Ao rematar a carreira, para enfrontarme ao que osmaba que sería o meu destino profesional, a docencia, procurei en diversos libros un punto no que agarrarme coa esperanza de que me desen algunha indicación de como asumir o reto baixo unhas directrices minimamente dignas. Non me estou referindo a libros texto, no único que podía achar era "o que", estaba á procura do "como". Daquela a oferta non era moi abondosa, pero percorrín moitos libros de divulgación, outros específicos de educación das matemáticas, dos que trataban da resolución de problemas, moitos sobre a historia e tamén algúns sobre filosofía da ciencia ou sobre a cultura matemática en xeral. Pero buscaba algo que, con todo, non daba atopado. Quizais porque tampouco sabía moito o que estaba a pescudar. Cando estou vendo o final do meu labor docente, por fin achei ese libro: "Xogando co infinito" de
Rózsa Péter (1905-1977). Felizmente este texto
foi publicado polo Consello da Cultura Galega (CCG), con tradución do profesor da Facultade de Matemáticias, Felipe Gago.
O pasado xoves 22/06/2023 presentouse a edición deste libro na aula magna da Facultade de Matemáticas. O primeiro que chama a atención é que no acto estivera presente Valentín García, o Secretario Xeral de Política Lingüística,
o mesmo que defende o decreto que prohíbe o ensino das matemáticas en galego. Por isto tanto a decana da Facultade de Matemáticas, Elena V. Cendón, como a presidenta do CCG, Rosario Álvarez, comezaron as súas intervencións cunha frase de Julio Rodríguez, presidente de AGAPEMA: "xa é hora de abrir unha fenda de luz e deixar de prohibir o galego no ensino das matemáticas". Valentín viuse na obriga de responder pero só conseguiu farfallar unha desculpa falsa, nun intento, imposible, de querer quedar ben.
Elena Vázquez Cendón explicou que o proxecto xurdira cando o premio Abel de 2005, Peter Lax, visitou Santiago de Compostela dentro do programa ConCiencia do 2007. Lax foi entrevistado pola periodista Elisa Álvarez quen, ante a idea de que todo matemático tivo alguén que o inspirou, inquiriulle sobre o seu caso. Peter Lax contestou que a súa inspiradora foi unha muller, Rózsa Péter, que escribira o mellor libro popular de matemáticas, "Xogando co infinito". Ao pouco Elena encargoulle o traballo de tradución a Felipe Gago. Hoxe, ademais da publicación física o CCG permite o acceso virtual a esta publicación.
Na súa intervención, Felipe Gago debullou, cunha fermosa presentación dixital, parte do contido do libro. Vou intentar reproducilo, quizais con algunhas modificacións.
Aprendiz de meiga
Todo comeza nunha aula. Susana, unha alumna que rebordaba curiosidade, Susana, comprobara que efectuar a suma de todos os naturais ata un impar, por exemplo 7, daba o mesmo resultado que multiplicar por 7 o número do medio.
Eva, unha compañeira da clase, deu coa chave do asunto. $4\cdot7$ non é outra cousa que sumar $4$ sete veces. Se comparamos as dúas sumas
Veremos que o primeiro $4$ é $3$ unidades superior a $1$, pero isto compénsase co último $4$, que é $3$ unidades inferior a $7$. Da mesma maneira o segundo $4$ é $2$ unidades máis que $2$, pero isto compénsase con que o penúltimo $4$ sexa $2$ unidades inferior a $6$. Finalmente o terceiro e o antepenúltimo $4$ son respectivamente $1$ unidadade máis e $1$ unidade menos que $3$ e $5$. Velaí que as dúas sumas teñan que dar o mesmo.
Neste punto Rózsa introduce a famosa lenda de como Gauss de neno, conseguira realizar a suma dos 100 primeiros números naturais: $1+2+3+4+....+96+97+98+99+100$. O proceso é esencialmente o mesmo que o que pasamos a describir para a suma dos 4 primeiros números. Coloquemos a suma tamén en orde inversa e despois sumemos o primeiro número co último, o segundo co penúltimo, e así sucesivamente. Así obtemos sempre $5$ como resultado
De aí que o dobre da suma buscada é igual a $5+5+5+5+5=4\cdot5=20$ polo que a suma será a súa metade $1+2+3+4+5=10$. Ademais este proceso, como vemos, non ten por que restrinxirse a sumas ata un número impar, como sucedía antes. Conviña repetir este proceso para outros casos como a suma dos 5 ou dos 7 primeiros números. Incluso podemos ver que podemos aplicalo a unha progresión aritmética calquera.
Neste caso a suma será a metade de $18\cdot5=90$, isto é $5+7+9+11+13=45$
Rózsa Péter non lles dá aos alumnos a fórmula para obter a suma dos termos duna progresión aritmética. Ofrécelle problemas que poden abordar e fainos protagonistas do seu descubrimento, ademais conecta ese achádego co mito gausiano facéndoos partícipes da historia das matemáticas. Isto xa sería suficiente, pero aínda hai máis. O método que vimos de presentar aparece noutros ámbitos das matemáticas. Todos sabemos como medir áreas de rectángulos.
Se tomamos como unidade o cadrado sombreado enseguida vemos que a área deste rectángulo é de $3\cdot8$, basta multiplicar a base pola altura para obtela. Pero enseguida xurde un problema. Se pretendemos obter a área dun triángulo como o seguinte
temos dificultades en completar a área sombreada. A solución vén de aplicar a mesma metodoloxía que a usada para achar as anteriores sumas. No canto dun triángulo, collamos dous, agora formarán un rectángulo
polo que para determinar a área do triángulo bastará con partir pola metade a deste novo rectángulo.
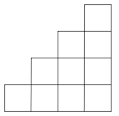
Se continuamos pola senda xeométrica, as anteriores sumas poderían representarse formando unha escaleira
Nesta figura temos representada a suma $1+2+3+4$. Volvamos a aplicar o mesmo procedemento, dupliquemos a figura e rotémola 180º, temos...
... un rectángulo de área $4\cdot5=20$ de aí que a suma buscada sexa, coma antes, 10.
En que circunstancias temos que sumar desde 1 ata un determinado número? Velaquí un problema que responde a esta cuestión
Problema. Determina o número de diagonais dun octógono
Unha boa maneira de abordalo é considerar unicamente os vértices do octógono e comezar a trazar todos os segmentos posibles entre eles. Se conseguimos facelo ao final só teriamos que restarlle os 8 lados do octógono. Comecemos polo vértice $1$, desde el podemos trazar sete segmentos ata os outros sete puntos; se continuamos co vértice $2$ veremos que agora xa só temos seis vértices aos que conectar con algún segmento
De continuarmos así, é evidente que o número total de segmentos que podemos trazar entre eses 8 puntos é $1+2+3+4+5+6+7=28$ polo que o número de diagonais serían $28-8=20$
Ao decatármonos de que cada segmento une dous puntos, veremos que estamos tratando co problema de como escoller dous elementos de entre 8. A este tipo de recontos chámaselle combinacións. Todas as posibles combinacións de dous elementos escollidos dentro dun conxunto de 8 pódense enumerar sistematicamente
$$\begin{matrix} & & & & & &12 \\ & & & & &23 &13 \\ & & & &34 &24 & 14\\ & & &45 &35 & 25 &15 \\ & & 56 &46 & 36 &26 &16 \\ &67 & 57 &47 & 37 &27 &17 \\ 78 &68 & 58 &48 &38 &28 &18 \end{matrix}$$
Cantas parellas vemos? Contando de esquerda a dereita $1+2+3+4+5+6+7$, ademais esta disposición forma unha escaleira, como a que repesentamos antes. Tamén poderiamos argumentar que cada un dos elementos pode emparellarse cos outros sete, co cal teriamos $8\cdot7$ parellas pero aparecerían duplicadas, de aí que o resultado teremos que dividilo por dous.
Vemos repetido, unha e outra vez o mesmo argumento e en distintos contextos. Velaquí a condensación de todo o que estivemos estudando
$$1+2+3+...+n=\frac{n\left ( n+1 \right )}{2}$$
Ademais, en todo este proceso aprendimos que é moito mellor deixar esta fórmula para o final. Así é como se aprenden, e como se deberían ensinar, as matemáticas.