Criptografía e maxia no Losada

Algún día tería que relatar as miñas desventuras no CAP (Curso de Adaptación Pedagóxiga), un curso que xogaba aproximadamente o mesmo papel que o Máster de Profesorado actual. Só comentarei que, cando me faltaba só unha sesión para rematalo, abandoneino, farto.  Efectivamente, estaba farto de ver como quen presumiblemente tiña que dar directrices sobre orientacións didácticas actuaba como un terrorista pedagóxico. Recordo unha materia levada por dous profesores, un home gordo e unha muller fraca. Impartían clase xuntos. Pasaban todo o tempo discutindo. Iso podería estar ben se fose algo pensado e preparado. Non era o caso.  Nunha ocasión pasaran toda a sesión dándolle voltas a como tratar aos rapaces zurdos. Se conviña, ou non, forzalos a escribir coa man dereita. Non era esta un tema que houbese que tratar no CAP, só foi unha ocorrencia máis desa parella infame de profesores. Desde aquela quedoume a impresión que unha clase levada en parella tiña que ser necesariamente un fracaso. Non é así. Isto demostráronolo Nicanor Alonso e Miguel Mirás o pasado venres 16/05/2025 na charla que viñeron impartir ao IES Antón Losada Diéguez ao alumnado de 1º de Bacharelato. O segredo do éxito dunha clase en tándem? O mesmo que o dunha clase impartida por unha persoa soa: traballo e preparación. 

O título da charla era "Historias e segredos da criptografía". Trataron temas como o da escritura xeroglífica, a reixa de Cardano, os acrósticos, a escítala espartana, o cifrado César ou o máis sofisticado de Vigenére,  sempre solicitando a participación e complidade do alumnado. Nicanor e Miguel repartiron unha roda como a da imaxe, que nos permitiu encriptar unha mensaxe seguindo as directrices dos dous últimos sistemas de cifrado. 

Examinaron moitos máis tópicos e sempre dunha forma clara e coordinada. Claro que, no canto de ser explicados en parella, tal e como o fixeron eles, case todos podían ter sido tratados por un só conferenciante. Comento isto porque un dos capítulos necesitaba de dúas persoas para poder desenvolvelo. A min foi o que máis me sorprendeu e agradou. Trátase do truco das 5 cartas de Cheney, asunto do que, por certo, xa se ocupara no seu día Jota nesta entrada, O mellor truco de cartas. O enunciado promete. Vexamos como se desenvolveu.

As cinco cartas de Cheney

Un dos dous conferenciantes marchou da sala; chamémoslle  mago. O outro, chamémoslle axudante,  pediu a un voluntario que escollera cinco cartas dunha baralla francesa completa (52 cartas, 13 de cada un dos paus, a saber: corazóns ♡ , diamantes ♢, picas ♠ e trevos ♣). Entón o axudante colocou catro desas cartas sobre unha mesa e deixou a quinta ao final, virada cara abaixo.

Cando volveu o mago e veu esas cartas sobre a mesa, concentrouse un momento e adiviñou cal era a carta que estaba boca abaixo.

Estaba claro que elaboraran un código para identificar as cartas pois diso trataba a conferencia. Pero teñamos presente que non poden saber previamente cales son as cartas que se van escoller polo que o código debería estar montado sobre a ordenación das cartas. Está claro que podemos establecer unha orde entre todas elas. En primeiro lugar, os números (do 1 ao 13) axudan moito. E que pasa se dúas cartas teñen o mesmo valor numérico? Daquela basta con que o mago e o seu axudante establezan unha orde dos paus. Podería ser, por exemplo, a orde do abecedario pola primeira letra: corazóns ♡ < diamantes ♢< picas ♠ < trevos ♣. Con todo, hai un problema, as $4$ cartas que quedan visibles só poden ordenarse de $4!=24$ formas distintas. 

Para salvar esta dificultade hai que aproveitar todas as vantaxes que nos dá o desenvolvemento do truco. Teñamos presente que é o axudante quen escolle a carta que se coloca boca abaixo. Polo principio do pombal, dadas $5$ cartas, é seguro que vai haber polo menos dúas do mesmo pau. Isto permite que o axudante escolla dúas cartas do mesmo pau e coloque unha cara abaixo e a outra pode colocala na primeira posición. No noso exemplo a primeira carta era o rei de trevos, velaí que a carta a adiviñar será tamén un trevo. Agora quédannos outras tres cartas visibles que nos deben permitir identificar o número da carta oculta. Outra vez, se ordenamos esas tres cartas termos un total de só $3!=6$ posibilidades e nós necesitamos 13. Aquí é onde entra en xogo a aritmética modular. 

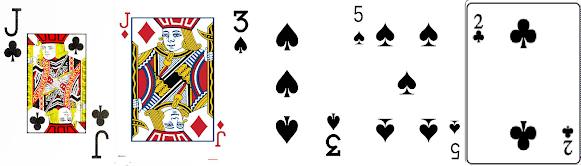
Facemos unha identificación do valor da carta cos números das congruencias de $\mathbb{Z}_{13}$. A diferenza entre dous destes valores nunca é maior que $6$. As cartas que escolleu o axudante eran a $J$ e o $2$ de trevos. A súa diferenza é de $4$ unidades. Ocultando o $2$ só lle ten que dicir ao seu compañeiro que debe sumarlle $4$ unidades á $J$. En aritmética modular $11+4\equiv 2 (mód 13)$. O código utilizado para indicar o número a sumar é o que explicamos de seguido. Vou identificar o $1$ co valor máis baixo das tres cartas, o $2$ co intermedio e o $3$ co maior. Daquela establezo a seguinte relación entre as $6$ ordenacións e o $6$ números que debo sumar (módulo 13) ao valor da primeira carta:

$$\begin{pmatrix} 1,2,3 & \longrightarrow 1 \\ 1,3,2 &\longrightarrow 2 \\ 2,1,3& \longrightarrow 3 \\ 2,3,1 & \longrightarrow 4 \\ 3,1,2& \longrightarrow 5 \\ 3,2,1 & \longrightarrow 6 \\ \end{pmatrix}$$

Como as tres cartas centrais son: $J$♢, $3$♠, $5$♠ vemos que a orde das cartas é: maior,  menor, intermedia que identificamos coa permutación $3,2,1$, de aí que o número a sumar é o $4$. Polo tanto o mago adiviña a carta oculta:

Principio do pombal, combinatoria e aritmética modular, todo dentro dun truco de maxia. 

Charlas científico-divulgativas

A Universidade de Vigo ofrece cada ano charlas científico-divulgativas. No seu folleto divulgativo acharemos epígrafes como os de "Ciencias da natureza", "Física e Química" ou "Economía". Aparentemente non se oferta ningunha charla de "Matemáticas". Eu aconsellaría aos centros de ensino de Secundaria buscar nese folleto os nomes de Nicanor Alonso e Miguel A. Mirás e concertar con eles unha actividade.

A revolución do "De Revolutionibus"

De revolutionibus orbium coelestium, ou máis brevemente De revolutionibus, é o volume, en seis libros, escrito por Copérnico (1473-1643) e publicado, coma quen di, póstumamente, no 1643 pois cóntase que cando saiu do prelo o autor xa estaba no seu leito de morte. Deste xeito tan tráxico o astrónomo presentaba públicamente o seu sistema dun mundo heliocéntrico. O escritor Arthur Koestler (1905-1983) cualificaríao no best-seller Os sonámbulos como "o libro que niñguén puido ler". As razóns desta descrición aséntanse na prosa técnica e pouco amable que destila o texto copernicano xa que a partir do segundo libro o texto é unha obra especializada de astronomía matemática que intentaba competir co Almaxesto de Ptolomeo e os seus epígonos. A confrontación entre os dous sistemas fundamentábase nunha serie de mecanismos matemáticos moi técnicos. Con toto, o apelativo de Koestler é moi inxusto xa que o De revolutionibus, desde o momento da súa publicación, sería un punto de referencia ineludible para os astrónomos posteriores. 

A Universidade de Vigo acaba de sacar do prelo O libro que ninguén puido ler, unha publicación cun título digno de Raymond Smullyan, elaborada polos matemáticos Nicanor Alonso e Miguel Mirás xunto co profesor, tradutor e poeta Raul G. Pato. Esta edición, xira arredor da tradución dun manuscrito do Libro I do De revolutionibus. Nese manuscrito non aparecían os tres últimos capítulos dese Libro I, precisamente os de contido matemático. En consecuencia, non se adentra nos esotéricos artefactos mecánico-astronómicos copernicanos senón que trata da exposición e argumentación dunha revolucionaria visión do mundo. Tan revolucionaria que se enfronta aos fundamentos ideolóxicos dominantes. Non se podía remover a crenza da inmobilidade da Terra sen que se visen afectadas as estruturas de poder que controlaban o coñecemento, a visión e a organización do mundo. Isto xa se sente desde un primeiro momento. Nas primeiras edicións do De revolutionibus aparecía un aviso Ao lector sobre as hipóteses desta obra que non foi redactado por Copérnico nin polo seu axudante Rheticus (1514-1574), senón polo substituto deste, o teólogo protestante Andreas Osiander, Sorprendentemente, neste curioso prólogo retíraselle toda a credibilidade ao corpo do libro:

"E non é necesario que estas hipóteses sexan verdadeiras, nin sequera verosímiles, senón que basta con que amosen tan só un cálculo congruente coas observacións"

Porén, unhas poucas páxinas máis adiante, Copérnico (agora si é el quen escribe) é moi claro:

"Se por casualidade aparecen rexoubeiros que, alegando ser capaces de emitir un xuízo sobre calquera cousa relacionada coas matemáticas, aínda sendo ignorantes delas e terxiversando maliciosamente algunha psasaxe da Escritura para o seu propósito, ousen atacar e rexeitar esta miña empresa, eu non fago caso deles ata o punto de desprezar o seu xuízo cualificándoo de temerario"

Velaquí que Copérnico non só tiña un coñecemento  profundo dos ceos, tamén era quen de desentrañar as reviravoltas da sociedade do seu tempo ata o punto que neste parágrafo parece adiviñar cal vai ser o futuro das teses do De Revolutionibus.  Efectivamente, se por unha banda Lutero e Calvino son os primeiros en opoñerse firmemente ao heliocentrismo, a igrexa católica prohíbe defendelo ou sostelo no ano 1616 ao tempo que inclúe a obra copernicana no índice de libros prohibidos. Esta foi a atroz resposta a unha convincente campaña de Galileo na que todos e cada un dos seus descubrimentos co telescopio son punzantes argumentos pro-heliocéntricos. A pesar das prohibicións da Igrexa Galileo non ficaría inmóbil. Nunca deixaría de argumentar contra a física aristotélica, o principal sustento do modelo ptolemaico. 

A  xenialidade de Galileo destaca especialmente no Diálogo, publicado no 1632 despois de entrevistarse co propio papa Urbano VIII e de que se lle impuxeran varias condicións. Obrigóselle a que cambiara o título: xa non sería Do fluxo e refluxo das mareas, senón Diálogo sobre os dous máximos sistemas do mundo. Outra esixencia consistía na inclusión dun aviso ao lector (outro máis!) no que se forzou a Galileo a declarar que adoptaba o copernicanismo como se fose unha hipótese puramente matemática. Tamén se lle impuxo a conclusión final do libro na que debían aparecer as teses de Urbano VIII establecendo que o infinito poder de Deus podía presentarnos os fenómenos de múltiples maneiras. Noutras palabras: a indagación científica é un inútil sinsentido. Ademais o Diálogo foi revisado polo Maestro do Sacro Palacio de Roma, con atribucións plenas para dar permisos de edición. Galileo aceptou todas as condicións, por inxustas que fosen. Con todo, ao pouco da publicación o Diálogo foi secuestrado e Galileo tivo que enfrontarse a un xuízo inquisitorial que o acabaría condenando.

A publicación da Universidade de Vigo ofrécenos como apéndices tanto a sentenza como a abxuración de Galileo Galilei. Son dous documentos de innegable importancia na historia da ciencia e un bo epílogo para O libro que ninguén puido ler. Como prólogo ofrécesnos un estudo sobre Copérnico e a súa obra. En definitiva, temos diante unha publicación que pon o foco nun capítulo central no desenvolvemento do pensamento científico. Tamén, por ser unha das escasas publicacións de temática científica en galego, unha contribución á dignificación da nosa lingua que todos deberiamos agradecer.

Os autores de Mate-glifos, unha gran vocación de divulgar as matemáticas

Nicanor Alonso e Miguel Mirás son dous profesores de matemáticas da Universidade de Vigo que escribiron un libro de divulgación titulado "Mate-glifos" (Xerais, 2019) do que temos falado neste mesmo blogue. O pasado 14 de marzo visitaron o IES Antón Losada (A Estrada) para ofrecer unha charla ao alumnado de 2º e de 4º da ESO. Ambos demostraron unha gran vocación de divulgación, unha actitude contínua de achegar as matemáticas aos rapaces botando man de múltiples recursos: ábacos, imaxes, xogos con números, un cubo máxico ou un simple folio.

Comezaron preguntando que é un mate-glifo. Esta palabra non existe nos dicionarios, pero si acharemos o termo glifo. Se sabemos o que é un petróglifo, ou un xeroglifo xa podemos enxergar o significado do vocablo mate-glifo. Efectivamente, estámonos referindo aos símbolos matemáticos. Os principais podémolos consultar neste póster que nos ensinaron no transcurso do seu relatorio. Vemos como a carón de cada símbolo temos o seu significado, quen e en que ano o usou por primeira vez. 

Póster Glifoteca by kiarqu2458

Durante as súas intervencións Nicanor e Miguel non só nos falaron dos símbolos matemáticos ou do significado da idea matemática de base dun sistema de numeración, senón que tamén compartiron diversos xogos matemáticos que desenvolvían as ideas matemáticas que estaban tratando.

Como se abordou o tema do uso do corpo humano como soporte para contar, presentouse un método para obter a táboa do 9 a partir dos dedos das mans. 

  

Nestas imaxes podemos ver ao alumnado en plena práctica de repaso da táboa de multiplicar.

Tamén se falu do sistema de numeración en base 2, e en relación con el, mediante o cubo das idades do matemago Werner Miller, os poñentes adiviñaron as datas de nacemento de varios alumnos. O cubo en cuestión é un artefacto moi curioso, con 5 das súas caras formando cadrados máxicos con números do 1 ao 31. Ademais cada un deses 5 cadrados máxicos verifica a propiedade de que todos os números que o forman comparte a propiedade de teren un 1 no mesmo lugar da súa escritura en forma binaria. Lembremos que un cadrado máxico consiste nunha táboa de 3x3, 4x4, 5x5,.... números de forma que a suma de todas as filas, a de todas as columnas e a das dúas diagonais dá sempre o mesmo resultado. Por exemplo, no cadrado máxico 4x4 da imaxe de abaixo, todas estas sumas dan 70. 

Mate-glifos, un libro para recomendar

Ano tras ano observaba con envexa como o profesorado de lingua galega recomendaba lecturas ao alumnado. Eu, non podía facer o mesmo se non era traizoando a miña lingua. Por fin, aínda que mínimamente, como lle corresponde a unha lingua minorizada, podo comenzar a facelo.
Ao contrario do que sucede coa contaminación luminosa, que está apagando as estrelas, a colección de Xerais Básicos Ciencia é a única luz nesta escuridade que afecta á normalización dentro divulgación científica.
Nesa colección vén de publicarse Mate-glifos (Xerais 2019), da autoría dos profesores do Departamento de Matemáticas da Universidade de Vigo Nicanor Alonso e Miguel Mirás. O primeiro deles é o autor doutro libro publicado este ano, A lista de Hilbert (UVigo, 2019), un texto que na súa parte principal podía consultarse na Biblioteca Virtual de Literatura Universal en Galego e que agora publicou a Universidade de Vigo con algunha engádega como os Problemas Clay. Nesta mesma biblioteca virtual atopamos unha tradución da que Nicanor Alonso é co-autor, a do Libro I dos Elmentos de Euclides. Por outra banda Miguel Mirás é un dos partícipes nun texto pensado para a docencia universitaria, Matemáticas á Boloñesa (UVigo, 2014) que tivo que ser ser reestruturado para adaptalo ás novas normas e esixencias, dando lugar a, Un mar de matemáticas (UVigo, 2016). Non é Mate-glifos a única colaboración destes dous autores pois xa se xuntaron para ofrecernos Arenarius, a tradución ao galego da obra de Arquímedes. Estamos, polo tanto, fronte a dous autores experimentados e cun aval no ámbito da escritura sobre o coñecemento matemático máis que certificado. Aínda máis, como demostran todas estas referencias anteriores ambos os dous están interesados e comprometidos coa normalización da lingua, valor que os fai merecedores de todo o noso agarimo.
 Pero, que son os mate-glifos? Se como resposta ofrecésemos unha outra pregunta: "que son os petróglifos?", de certo que colleríamos o fío de por onde van as cousas. Un glifo, RAG dixit, é "un signo ou debuxo de carácter simbólico empregado en diferentes sistemas de escritura". Velaí que este libro está adicado á escritura dos algarismos (1, 2, 3, 4, 5, 6, 7, 8, 9 e 0), mais tamén doutros símbolos matemáticos como o punto ou a coma decimais, as parénteses, corchetes ou chaves como glifos de agrupamento,  +, ー, ✕ ou ⋅, ÷ ou a/b, √, a^b, r॥ s (r paralela a s), r丄s (r perpendicular a s), ＞, ＜, =, x como incógnita, as abreviaturas trigonométricas sen, cos e tan, log como abreviatura de logaritmo, ∑, Π,  f ', ∫, ou os números e, π, i.
Quen propuxo toda esta simboloxía?, cando? cales son as razóns da escolla actual? Nicanor Alonso e Miguel Mirás intentan responder a estas cuestións.Teñamos presente que a resposta nunca é inmediata. Todas as ideas que gardan estes glifos escribíronse de distintas maneiras dependendo da época e incluso do autor. Consideremos por exemplo o símbolo da igualdade (=). Escollino porque, segundo a miña experiencia,  o creativo alumnado de secundaria está empeñado en substituílo por frechas (➝). Cada vez que o fan preséntolles a Robert Recorde, quen no 1557 expresou o seu argumento para introducir o símbolo = e que viaña sendo que el non era que de imaxinar dúas cousas máis iguais que dúas paralelas. En Mate-glifos faise referencia a outras escrituras para representar a igualdade tales como Ч (copistas do III e IV), pha, aeq., ae, ...
Aínda hai outra característica deste libro que o fai máis atractivo. Tomando como desculpa os tópicos que vai tratando, introdúcense a modo de pílulas, cuestións de carácter divulgativo. Esta estratexia de elaboración do libro faino moito máis dinámico para o lector que busca algo máis que unha restra de explicacións sistemáticas sobre a escritura matemática. Ao falarnos dos símbolos da división explícase en que consiste a proba do 9 (teño que confesar que é a primeira vez que a vexo nun texto impreso). A carón do sistema de numeración binario detállase un truco de maxia que utiliza este sistema. Os logaritmos van acompañados do problema do coleccionista de cromos: cantos cromos se espera que teña que comprar para completar unha colección de 200? A resposta, que recollo do libro, é de 1176. Noutro capítulo, a raíz da demostración do teorema de Pitágoras coñecida como a cadeira da noiva, preséntasenos un quebracabezas de Henry Dudeney consistente en cortar un triángulo equilátero en 4 pezas de forma que ao volver a xuntalas poidamos formar un cadrado.

Velaquí o triángulo equilátero, recórtao e forma un cadrado

Como regalo final, ofrécesenos un pequeno dicionario etimolóxico dalgúns termos matemáticos e unha táboa (ou glifoteca) con símbolos, ano de aparición e autor. Non sei que esperades para ler e, xa que logo, recomendar.