O (mate)mago que presentaba o xogo era Victor Eigen. Un espectador, que non era outro que Martin Gardner, ofreceu a súa propia baralla para que o mago non tivese posibilidade de marcar as cartas. O espectador escolleu 5 cartas e (isto é unha diferenza importante coa versión relatada aquí) escolleu tamén cal desas 5 cartas se debía adiviñar. O único que podía facer o mago era ordenar as outras $4$ cartas. Nesa orde leváronllas á muller de Eigen, que se hospedaba nunha habitación do hotel que albergaba o congreso. E a muller acertou a carta escollida! Como podía ser? $4$ cartas só podemos ordenalas de $24$ formas distintas. Parecía imposible que Eigen e a súa muller poidesen elaborar un código para as 52 cartas.
A resposta é a seguinte. En primeiro lugar, como á señora Eigen lle entregaban $4$ cartas xa non tiña que buscar a carta escollida entre as $52$ da baralla. Quedábanlle $52-4=48$ pero os Eigen só podían elaborar un código para a metade deste montón, $24$. A trampa era que o matrimonio reservara dúas habitacións contiguas e Victor non desvelou o número da habitación ata que Gardner escolleu a carta que debía adiviñar a señora Eigen. Cando Gardner petou nunha das portas para entregar as $4$ cartas, a muller de Victor puido descartar $24$
O truco orixinal
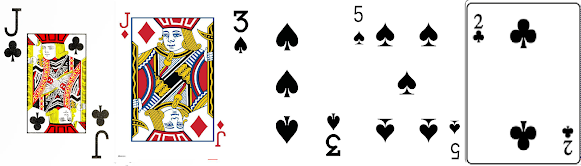
Volvamos ao truco orixinal, que apareceu nun artigo do ano 1950 na revista Math Miracles e no que lle atribuían a invención a Fitch Cheney. Lembremos as condicións. O mago marcha da habitación. Un espectador escolle $5$ cartas e o axudante do mago dálle a volta a unha desas $5$ cartas e colócaa á dereita das outras $4$ que fican cara arriba. Como é o axudante quen escolle a carta a adiviñar, podemos usar este feito para dar máis información ao mago-vidente. Na experiencia que relatamos da adiviñación no IES Antón Losada o axudante escollía unha carta do mesmo pau que a oculta. Isto reduce as posibilidades nun factor $4$ pero pode facerse mellor e as $P_{4}=4!=24$ posibilidades de ordenación das cartas poden chegar a multiplicarse por un factor $5$ á hora codificar toda a información. Ademais, ao estaren á vista $4$ cartas o mago sabe que a oculta non pode ser ningunha desas. De aí que o truco das $5$ cartas permitiría realizar a adiviñación nun mazo de $5\cdot 4!+4= 5!+4=124$ cartas. Neste artigo, Using a card trick to teach discrete mathematics, Shai Simonson e Thara S. Holm mostran como facelo. Daquela podemos considerar en xeneralizar o truco para un mazo de $m$ cartas do que extraemos $n$ e despois, de entre estas $n$ o axudante escolle unha para que sexa a carta oculta. Así o mazo podería ter $m=n\cdot (n-1)!+n-1=n!+n-1$ cartas [1]. Na seguinte táboa mostramos os primeiros valores.
| $n$ | $m=n!+n-1$ |
|---|---|
| $1$ | $1$ |
| $2$ | $3$ |
| $3$ | $8$ |
| $4$ | $27$ |
| $5$ | $124$ |
| $6$ | $725$ |
Claro que o valor de $m$ podería ser menor. Se podemos establecer unha codificación para os valores de $m$ dados na táboa anterior, é evidente que tamén se poderá facer se o tamaño do mazo é inferior a $m$. Por exemplo, no caso relatado cando presentamos o truco de Cheney, o mazo era normal, tiña $m=52$ cartas, cando para $n=5$, tal e como queda establecido nesta táboa, poderiamos facer o truco para un total de $m=124$ cartas.
Coa finalidade de afacernos ao problema, estudaremos os primeiros casos. Para $n=2$ e $m=3$ a codificación é trivial.
| 12 | 13 | 23 |
|---|---|---|
| 1 | 3 | 2 |
As cartas ocultas son as que aparecen en branco con fondo negro. Así, se o espectador escolle o par $1,2$, o axudante dálle a volta á carta $2$ e o mago ao ver cara arriba a carta $1$ xa sabe que está oculto o $2$
Para o seguinte valor, $n=3$, $m=8$ as cousas xa se complican bastante. O espectador terá $C_{8,3}=\binom{8}{3}=56$ formas posibles de escoller 3 cartas. Agora o axudante debe deixar dúas delas cara arriba nunha determinada orde. Hai un total de $A_{8,2}=56$ arranxos, isto é, formas de escoller $2$ cartas ordenadas no mazo de $8$. Os valores coinciden, pero será posible establecer un código para cada caso? Teñamos presente que o código está formado por dúas cartas ordenadas, pero esas dúas cartas teñen que escollerse entre as $3$ determinadas polo espectador. Neste caso pódese facer tal e como vemos na seguinte táboa. Se o espectador colleu as cartas $123$ o axudante tapa a última e deixa as outras na orde indicada na segunda fila $1,2$. Se a orde fose $2,1$ o mago sabería que a carta oculta tería que ser un $4$.
| 123 | 124 | 134 | 135 | 145 | 146 | 125 | 156 |
|---|---|---|---|---|---|---|---|
| 1,2 | 2,1 | 1,3 | 3,1 | 1,4 | 4,1 | 1,5 | 5.1 |
| 126 | 136 | 127 | 137 | 128 | 138 | 234 | 235 |
| 1,6 | 6,1 | 1,7 | 7,1 | 1,8 | 8,1 | 2,3 | 3,2 |
| 245 | 246 | 256 | 257 | 236 | 267 | 237 | 247 |
| 2,4 | 4,2 | 2,5 | 5,2 | 2,6 | 6,2 | 2,7 | 7,2 |
| 238 | 248 | 345 | 346 | 356 | 357 | 367 | 368 |
| 2,8 | 8,2 | 3,4 | 4.3 | 3,5 | 5,3 | 3,6 | 6,3 |
| 347 | 378 | 348 | 358 | 456 | 457 | 467 | 468 |
| 3,7 | 7,3 | 3,8 | 8,3 | 4,5 | 5,4 | 4,6 | 6,4 |
| 147 | 478 | 148 | 458 | 567 | 568 | 157 | 578 |
| 4,7 | 7,4 | 4,8 | 8,4 | 5,6 | 6,5 | 5,7 | 7,5 |
| 158 | 258 | 167 | 678 | 168 | 268 | 178 | 278 |
| 5,8 | 8,5 | 6,7 | 7,6 | 6,8 | 8,6 | 7,8 | 8,7 |
Poderemos establecer sempre un código? Ao escoller o código $(1,2)$ para 123 estamos imposibilitando que este código nos identifique os casos 124, 125,... 128 polo que todas estas escollas deben ser codificadas con outros pares ordenados de números que poderían ser $(1,4)$, $(1,5)$,..., $(1,8)$ pero estas novas escollas permitirán establecer un código distinto para as posibilidades que faltan? Haberá algunhas asignacións que nos impidan colocar as últimas identificacións.
O seguinte caso, o de $n=4$ e $m=27$ xa daría lugar a unha táboa codificadora de $C_{27,4}=\binom{27}{4}=A_{17,3}=17550$ elementos.
En xeral o código poderá crearse se hai unha relación biunívoca entre todas as posibles escollas do espectador que suman un total de $C_{m,n}=\binom{m}{n}$ posibilidades, e as ordenación de $n-1$ cartas que faga o axudante. Este último valor contabilízase mediante os arranxos $A_{m,n-1}=m\cdot (m-1)\cdot ... \cdot (m-n+2)$. Se igualamos estas expresións:
$$C_{m,n}=\binom{m}{n}=\frac{m!}{n!(m-n)!}=A_{m,n-1}=\frac{m!}{(m-n+1)!}$$
Igualando denominadores e operando:
$$(m-n+1)!=n!(m-n)!$$ $$\frac{(m-n+1)!}{(m-n)!}=n!$$ $$m-n+1=n!$$ $$m=n!+n-1$$
Velaí que os dous conxuntos teñen o mesmo cardinal cando a cantidade de cartas do mazo é a que determinaramos previamente en [1]. A cuestión sería entón se se poderá establecer unha codificación da información dada polo protocolo do xogo para poder levalo a cabo en todos os casos. Unha opción sería a de elaborar un algoritmo que cree unha codificación para calquera caso. Esta sería a resposta escollida por un informático. Pero hai un achegamento máis bonito, o derivado do punto de vista matemático. Non nos dá a solución, pero hai un teorema da teoría de grafos que nos permite asegurar a existencia da codificación. O teorema é o seguinte.
Teorema de Hall. Dado un grafo bipartito $G=(X,Y)$, unha condición necesaria e suficiente para que $X$ teña un emparellamento perfecto (condición de Hall) é que $\forall A\subset X$ se verifique que $ \left| A \right|\le \left| N\left( A \right) \right|$
Cómpre aclarar notación e conceptos para entendermos o teorema. Un grafo $G$ dise bipartito se pode descompoñerse na unión disxunta de dous conxuntos de vértices $X$ e $Y$ tales que os vértices de $X$ só se conectan con vértices de $Y$ (e viceversa). $N\left( A \right)$ fai referencia á veciñanza de $A$, isto é, o conxunto de vértices que están conectados con algún elemento de $A$. As barras verticais indican o cardinal. Un emparellamento $M$ dun grafo $G$ é unha colección de arestas que non teñen ningún vértice en común. Dise que un emparellamento SMS é perfecto se todos os vértices do grafo son extremo dalgunha aresta de $M$.
Consideremos o caso xeral. Temos $m=n!+n-1$ cartas distintas, o espectador escolle $n$ e o axudante dálle a volta a unha delas e ordena as restantes. Imos ver que poderemos establecer unha relación biunívoca (ou emparellamento perfecto) entre as $C_{m,n}$ escollas e as $A_{m,n-1}$ codificacións. Para iso consideramos o grafo bipartito $G=(X,Y)$ onde os vértices de $X$ serán cada unha das posibles combinacións e os de $Y$ cada un dos posibles arranxos. As arestas conectan cada combinación de $n$ elementos de $X$ con todas as posibles ordenacións de $n-1$ elementos desa combinación. Por exemplo na codificación anteriormente estudada para $n=3$ e $m=8$, a combinación 1-2-3 estaría conectada coas permutacións de dous elementos escollidos en {1,2,3}: (1,2), (2,1), (1,3), (3,1), (2,3) e (3,2). Son un total de $n!=3!=6$ elementos. Da mesma maneira se consideramos un arranxo calquera, como (1,2) veremos que estará conectado coas 6 combinacións 1-2-3, 1-2-4, 1-2-5, 1-2-6, 1-2-7 e 1-2-8. Todos os vértices do grafo terán o mesmo grao, $6$. No caso xeral todos os vértices terán grao $n|$. Este tipo de grafos, nos que todos os vértices teñen o mesmo grao, chámanse grafos regulares. Vexamos que este grafo verifica a condición de Hall.
Efectivamente. Supoñamos que non a verifica, isto é, que existe un subconxunto $A\subset X$ de $k$ vértices que está conectado cun subconxunto de arranxos que ten menos de $k$ vértices. Como o grao de cada elemento é $n!$ a este subconxunto de arranxos, $N\left( A \right)$, deben chegar $n!\cdot k$ arestas. Velaí que polo principio do pombal ten que haber un arranxo ao que cheguen polo menos $n!+1$ arestas, o que entra en contradición con que todos os vértices tiñan grao $n!$.
Conviña decatarse de que non só demostramos a existencia de codificación para calquera truco estilo Cheney senón que acabamos de dar a proba do seguinte resultado:
Corolario. Sexa $G=(X,Y)$ un grafo bipartito regular. Daquela $G$ ten un emparellamento perfecto.
De querermos establecer un código completo para o truco de Cheney orixinal deberiamos cubrir unha táboa con $\binom{53}{5}=2.869.685$ celas!. Xa comprobáramos que para esta viaxe non cómpren tales alforxas. Con todo, como para unha escolla de $5$ cartas por parte do espectador temos asegurada a existencia dun código incluso cando o mazo ten $124$ cartas, a cantidade de emparellamentos codificadores para este valor tan baixo ($5$) xa subiría ata un total de $\binom{124}{5}=225.150.024$. Pode parecer sorprendente, pero neste pequeno traballo de Michael Kebler establécese un atallo para evitar tremenda tarefa.
O teorema de Hall recibe tamén o nome do teorema do matrimonio. Na seguinte entrada centrarémonos neste aspecto, na súa relación co problema dos matrimonios. O resultado foi demostrado polo matemático inglés Philip Hall (1904-1982), gran impulsor da teoría de grupos. Foi un dos participantes en Blettchley Park no traballo de descodificación de mensaxes durante a II Guerra Mundial.