Impactante e educativa curta. As matemáticas sempre estiveron no punto de mira das políticas educativas co fin de usar o prestixio que lle fornecían os seus esotéricos símbolos para proveito das máis variadas (e en moitos casos escuras) causas. Lembremos, por exemplo, que a gran revolución educativa no ensino da ciencia dos números que se quixo impulsar coa implantación nos anos 70 da matemática moderna, naceu como resposta nos países da órbita da OTAN ao gran sock que supuxo o programa Sputnik da Unión Soviética nun escenario de guerra fría. Hoxe as matemáticas son a punta de lanza do grupo de materias troncais, as áreas de coñecemento privilexiadas que o programa involucionista do PP está a impoñer nas nosas escolas. Aos nosos gobernos non lles importa nada o ensino das matemáticas. Os seus intereses están na permanencia no poder e para iso cómprelles dirixir un control ideolóxico que o faga posible. Por medio do decreto de plurilingüismo e a LOMCE os gobernos de Galicia e España só pretenden facer uso do prestixio das matemáticas como base do desenvolvemento científico para estableceren políticas nefastas desde punto de vista educativo, e en definitiva, con consecuencias moi negativas para a sociedade do futuro. En Galicia estase a usar a formación en matemáticas como arma contra a normalización lingüística. Con cada clase de matemáticas impartida en castelán estase a ensinar tamén que o galego é unha lingua de segunda categoría, da que se pode prescindir para o desenvolvemento científico e, en definitiva, inútil socialmente. En Galicia estase a ensinar que "dos más dos es igual a cinco"
sábado, 8 de decembro de 2012
2+2=5. As matemáticas contra a normalización lingüística
Impactante e educativa curta. As matemáticas sempre estiveron no punto de mira das políticas educativas co fin de usar o prestixio que lle fornecían os seus esotéricos símbolos para proveito das máis variadas (e en moitos casos escuras) causas. Lembremos, por exemplo, que a gran revolución educativa no ensino da ciencia dos números que se quixo impulsar coa implantación nos anos 70 da matemática moderna, naceu como resposta nos países da órbita da OTAN ao gran sock que supuxo o programa Sputnik da Unión Soviética nun escenario de guerra fría. Hoxe as matemáticas son a punta de lanza do grupo de materias troncais, as áreas de coñecemento privilexiadas que o programa involucionista do PP está a impoñer nas nosas escolas. Aos nosos gobernos non lles importa nada o ensino das matemáticas. Os seus intereses están na permanencia no poder e para iso cómprelles dirixir un control ideolóxico que o faga posible. Por medio do decreto de plurilingüismo e a LOMCE os gobernos de Galicia e España só pretenden facer uso do prestixio das matemáticas como base do desenvolvemento científico para estableceren políticas nefastas desde punto de vista educativo, e en definitiva, con consecuencias moi negativas para a sociedade do futuro. En Galicia estase a usar a formación en matemáticas como arma contra a normalización lingüística. Con cada clase de matemáticas impartida en castelán estase a ensinar tamén que o galego é unha lingua de segunda categoría, da que se pode prescindir para o desenvolvemento científico e, en definitiva, inútil socialmente. En Galicia estase a ensinar que "dos más dos es igual a cinco"
xoves, 22 de novembro de 2012
A utlidade da terminoloxía matemática en galego
A Comisión de Normalización Lingüística da Facultade de Matemáticas da USC promove unha rolda de discusión de terminoloxía matemática: o LEXI_GA_MATH, aberta a todos os interesados no uso correcto do vocabulario específico desta ciencia. Esta anotación quer ser tamén unha invitación a apuntarse nesta lista a todos os interesados en fornecernos dunha terminoloxía correcta no ámbito das matemáticas. Apelo a un interese que non se pode desligar do uso. Para iso paso a facer algo de memoria.
Principios
No ano 1979 publícase o que , segundo o seu editor, Xulián Maure, sería o primeiro libro "non só de Europa, senón do mundo enteiro, dedicado ó ensino das matemáticas en galego". Tratábase dun libro de texto para 1º de bacharelato, elaborado por un grupo de máis de medio cento de profesores coñecido como Colectivo Vacaloura. Os seus integrantes tiveran que facer o traballo sen referencia terminolóxica algunha. A súa achega respondía a unha necesidade imperiosa da sociedade galega de prestixiar unha lingua prohibida, a súa lingua. Para continuar este traballo e facelo como correspondía, con rigor científico, precisábase un vocabulario de termos especializados que fose o resultado dun traballo que non nos aportara simples traducións do castelán. Compría que alguén que sentira a lingua e con coñecementos da área dera o primeiro paso. Velaí que por fin no ano 1995 se presenta na Facultade de Matemáticas un libro editado pola USC e coordinado por X. M. Masa Vázquez e A. B. Fortes López. O seu título: Vocabulario de Matemáticas. [Pode descargarse o documento de texto desde aquí.]. O amigo e compañeiro Manuel Vilariño tivo a feliz idea de subilo á plataforma Scribd para que a súa consulta fose máis accesible a todos
A utilidade da terminoloxía matemática en galego. A cuestión central que se suscita despois de comprobarmos que dispoñemos de toda unha serie de recursos para establecer o vocabulario matemático é: para que queremos todo isto? A Secretaría Xeral de Política Lingüística (SXPL) financia a base de datos bUSCatermos. Pola contra esa mesma SXPL é o maior valedor do decreto que prohíbe o uso do galego no ensino das matemáticas que é precisamente o eido natural que lle pode dar máis valor e uso a toda esta recompilación terminolóxica. En ningún outro caso se pode ver con máis claridade unha das características fundamentais da política lingüística dos úlitmos anos. Trátase dunha política que parte de considerar ao galego como unha lingua de museo. Algarismo, alxébrico, arranxo ... Que triste é ver todos eses termos disecados! Contra unha política lingüística forense debemos propugnar unha medicina de habitos saudables pois única postura coherente é a que correlaciona interese pola lingua co seu uso. Temos que recuperar a necesidade imperiosa de prestixiar unha lingua prohibida e iso pasa por impartir as aulas de matemáticas en galego.
Principios
No ano 1979 publícase o que , segundo o seu editor, Xulián Maure, sería o primeiro libro "non só de Europa, senón do mundo enteiro, dedicado ó ensino das matemáticas en galego". Tratábase dun libro de texto para 1º de bacharelato, elaborado por un grupo de máis de medio cento de profesores coñecido como Colectivo Vacaloura. Os seus integrantes tiveran que facer o traballo sen referencia terminolóxica algunha. A súa achega respondía a unha necesidade imperiosa da sociedade galega de prestixiar unha lingua prohibida, a súa lingua. Para continuar este traballo e facelo como correspondía, con rigor científico, precisábase un vocabulario de termos especializados que fose o resultado dun traballo que non nos aportara simples traducións do castelán. Compría que alguén que sentira a lingua e con coñecementos da área dera o primeiro paso. Velaí que por fin no ano 1995 se presenta na Facultade de Matemáticas un libro editado pola USC e coordinado por X. M. Masa Vázquez e A. B. Fortes López. O seu título: Vocabulario de Matemáticas. [Pode descargarse o documento de texto desde aquí.]. O amigo e compañeiro Manuel Vilariño tivo a feliz idea de subilo á plataforma Scribd para que a súa consulta fose máis accesible a todos
Mates from Manuel Vilariño
As matemáticas en galego comenza a ocupar o seu lugar
De certo que este traballo contribuíu en moi boa medida a que a edición de libros de texto de matemáticas en galego nos anos seguintes se fixera de forma máis coordinada e pisando en chan firme.
É o caso que cos comenzos do século XXI as normalización comenza a notarse no eido do ensino das matemáticas. Todas as editoriais que querían estar realmente presentes nos centros escolares, tiñan que ter o seu libro de matemáticas en galego. Isto contribuiría a que tradutores, pedagogos, profesores, e moitos outros profesionais desenvolveran un traballo que se agradecía acotío nas aulas. As matemáticas comenzaban a andar o seu viaxe da man da normalización lingüística, sobre todo co impulso dado polo decreto 124/2007 que establecía que o ensino das matemáticas se desenvolvería en galego. Esta decisión non foi otra cousa que a ratificación do que se indicaba no PXNLG, aprobado por todos os grupos políticos do parlamento galego no ano 2004.
Desta época temos dous traballos máis, desta vez da Universidade da Coruña, incluídos dentro dun listado de vocabularios que desenvolven a campaña 'Profesionaliza a túa lingua', gañadora do primeiro premio Luísa Vilalta ás iniciativas normalizadoras. Estámonos a referir a:
- Pérez Vázquez, L.; P. Precedo Estraviz; N. Seoane Bouzas (2006): Profesionaliza a túa lingua: matemática. A Coruña: Universidade da Coruña. [Accesible en liña desde aquí].
- Pereiro Felípez, M. C. et alii (2008): Profesionaliza a túa lingua: estatística. A Coruña: Universidade da Coruña. [Accesible en liña desde aquí].
A utilidade da terminoloxía matemática en galego. A cuestión central que se suscita despois de comprobarmos que dispoñemos de toda unha serie de recursos para establecer o vocabulario matemático é: para que queremos todo isto? A Secretaría Xeral de Política Lingüística (SXPL) financia a base de datos bUSCatermos. Pola contra esa mesma SXPL é o maior valedor do decreto que prohíbe o uso do galego no ensino das matemáticas que é precisamente o eido natural que lle pode dar máis valor e uso a toda esta recompilación terminolóxica. En ningún outro caso se pode ver con máis claridade unha das características fundamentais da política lingüística dos úlitmos anos. Trátase dunha política que parte de considerar ao galego como unha lingua de museo. Algarismo, alxébrico, arranxo ... Que triste é ver todos eses termos disecados! Contra unha política lingüística forense debemos propugnar unha medicina de habitos saudables pois única postura coherente é a que correlaciona interese pola lingua co seu uso. Temos que recuperar a necesidade imperiosa de prestixiar unha lingua prohibida e iso pasa por impartir as aulas de matemáticas en galego.
xoves, 8 de novembro de 2012
'Isto é matemática'. Programa de divulgación da TV portuguesa
Un que sempre anda na procura de materiais de matemáticas en galego fiquei gratamente sorprendido ao enterarme de que na canle portuguesa de televisión SIC Notícias, comenzou a emisión dun mini-espazo de divulgación matemática: 'Isto é matemática'. O programa emítese os sábados ás 20:50. Condúceo o matemático Rogério Martins con simpatía e procurando facer accesible esta ciencia a todos os públicos. Así se presenta:
A matemática vai muito para além dos números e das equações. A matemática são ideias. Ela acontece sempre que há um padrão... Sempre que algo se repete... no seu quotidiano, nas ruas, no trânsito. São ideias que se materializam em todos os objectos que alguma vez observou... e talvez nunca tenha dado conta. A matemática é vida. A sua vida... e a minha.Sou o Rogério Martins... e sou matemático.'Isto é matemática' está promovido pola Sociedade Portuguesa de Matemática (SPM). Os programas emitidos ata o momento tráenme á cabeza o Ben Falado! da TVG, quizais pola pouca duración que teñen. Isto, no canto de ser un desventaxa, creo eu, é o seu maior valor. Cun guión e unha realización moi coidadas cada un destes capítulos é unha perla da divulgación matemática. Eu non os perderei de vista. Podemos seguir as novidades do programa nunha conta de facebook ou no seu portal da canle de televisión. Capítulo 1. Reinventar a roda. Capítulo 2. Como é que o google goola Capítulo 3. O bilhar, o dentista e o Teatro São Carlos Capítulo 4. O efeito borboreta
martes, 6 de novembro de 2012
Calculadoras: de Leonardo da Vinci a Ramón Verea
O Día da Ciencia en galego instaurouse como protesta contra o decreto de plurilingüismo que exclúe o galego do ensino das ciencias e da tecnoloxía. Na súa terceira edición escollénronse para centrar as actividades as figuras de Leonardo da Vinci e Ramón Verea.
Como aportación ás reivinidcacións da celebración do III Día da Ciencia en galego vai esta anotación sobre a historia das máquinas de cálculo desde Leonardo da Vinci (1493) ata Ramón Verea (1978).
O boceto de Leonardo da Vinci
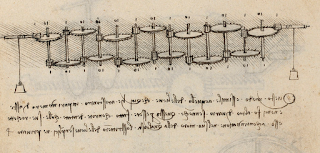
Cun total dunhas 700 páxinas, no ano 1967 descúbrense na Biblioteca Nacional de Madrid os documentos que serían coñecidos como Códice de Madrid I e II. O seu autor era Leonardo da Vinci (1452-1519). No folio 36-verso do tomo I atopamos un debuxo dun mecanismo de transmisión mediante un engranaxe no que a relación de transmisión é de 1:10. Por cada 10 voltas que lle deamos a unha roda, a seguinte moverase unha décima parte. Como segundo o esquema de Leonardo, a máquina consta de 13 unidades ensambladas, para que se mova un dente da última cómpre que que deamos 1.000.000.000.000 (un billón) de voltas á primeira roda. No seguinte vídeo vemos unha versión dixital deste aparato con 7 rodas no canto de 13.
 Ao pouco deste achádego o enxeñeiro Roberto A. Guatelli (1904-1993), experto mundial na obra de Leonardo da Vinci constrúe unha calculadora basándose no anterior esquema do Códice de Madrid I. Guatelli estaba especializado na construción de réplicas das máquinas de Leonardo, porén nesta ocasión ademais das indicacións do folio 36-verso Guatelli fai uso doutros mecanismos descritos tamén por da Vinci no Códice Atlántico pero que non eran da súa invención pois xa aparecían nun libro de Vitrubio do século I a. C. Con esta base constrúe unha calculadora para unha exposición da IBM que pretendía ser unha réplica do boceto de Leonardo pero á que se lle ven unha chea de defectos: nos comenzos do XVI non ten ningún sentido unha calculadora con tantas cifras; non hai ningunha marca numérica; tampouco se enxerga ningún mecanismo para introducir novos sumandos, o rozamento que se produciría sería tal que ao cabo dunhas poucas voltas resultaría imposible mover a maquinaria,....
Ao pouco deste achádego o enxeñeiro Roberto A. Guatelli (1904-1993), experto mundial na obra de Leonardo da Vinci constrúe unha calculadora basándose no anterior esquema do Códice de Madrid I. Guatelli estaba especializado na construción de réplicas das máquinas de Leonardo, porén nesta ocasión ademais das indicacións do folio 36-verso Guatelli fai uso doutros mecanismos descritos tamén por da Vinci no Códice Atlántico pero que non eran da súa invención pois xa aparecían nun libro de Vitrubio do século I a. C. Con esta base constrúe unha calculadora para unha exposición da IBM que pretendía ser unha réplica do boceto de Leonardo pero á que se lle ven unha chea de defectos: nos comenzos do XVI non ten ningún sentido unha calculadora con tantas cifras; non hai ningunha marca numérica; tampouco se enxerga ningún mecanismo para introducir novos sumandos, o rozamento que se produciría sería tal que ao cabo dunhas poucas voltas resultaría imposible mover a maquinaria,....
O reloxo de Schickard
Por todo o exposto considérase que a primeira máquina de calcular foi construída no 1623 por Wilhelm Schickard (1692-1635) un astrónomo alemán. O seu reloxo de cálculo podía realizar as catro operacións básicas. Pero o único que se construiu foi destruído nun incendio no 1624 seguramente nun incendio provocado por alguén que non soportaba que a máquina fose quen de realizar as mesmas operacións que "un espíritu sagrado e inviolable" do ser humano. Velaquí unha reconstrucción do reloxo calculador de Schikard a partir dun esquema recollido dunha carta que lle enviou ao eminente astrónomo Kepler:
A pascalina
No ano 1642 o filósfo e matemático francés Blaise Pascal (1623-1662) presenta unha máquina aritmética que realizaba sumas e restas. Construíronse varios exemplares que se distribuíron por Europa e servirían como referencia para que outros construíran as súas propias sumadoras.
A máquina de Leibniz
O maior defecto da pascalina era que non podía realizar produtos e divisións. Para superar esta limitación Gottfried Wilhelm Leibniz (1646-1716) , matemático, filósofo e diplomático alemán elabora unha máquina moito máis complexa que a de Pascal. Constrúe un exemplar no 1694 e outro no 1704, pero os seus mecanismos, demasiado complexos para o desenvolvemento tecnolóxico da época, nunca chegaron a funcionar satisfactoriamente. De todas formas, as innovacións que achegadas por Leibniz habían de ser utilizadas polos seguintes inventores.
O aritmómetro
Seguramente o deseño máis importante realizado sobre a base da calculadora de Leibniz sexa o aritmómetro. Esta calculadora ideada por Charles-Xavier Thomas de Colmar (1785-1870), un enxeñeiro francés que era director dunha compañía de seguros en París. A primeira versión foi contruída no 1822. Foi a primeira calculadora con éxito comercial de toda a historia, a súa produción estederase con sucesivas versións desta máquina durante todo o século XIX, incluso despois da morte de Thomas de Colmar, ata o ano 1915.
A multiplicadora de Ramón Verea.
Todas as caculadoras construídas ata o último cuarto do XIX tiñan un evidente incoveniente. Basaban o cálculo do produto nunha serie de sumas sucesivas. Ademais este procedemento non era automático. Todo isto cambiou coas aportacións que fixo Ramón Verea (1833-1899), cando no ano 1878 patentou en Nova York un mecanismo que podía realizar directamente multiplicacións cunha capacidade de obter resultados de ata quince cifras. Ramón Verea era plenamente consciente de cal fora a súa aportación á tecnoloxía das máquinas calculadoras. Nun artigo publicado no xornal Las Novedades de Nova York Verea afirmaba que
Para saber máis:
The history of computing project
arithmometre.org
History of computers Rechnerlexikon. Die große Enzyklopädie des mechanischen Rechnens
Códice de Madrid
Storia d´ell informatica, pdf didáctico
Ramón Verea. Inventor estradense, libro de Olimpio Arca Caldas
Historia universal de las cifras, libro de Georges Ifrah, editado por Espasa
Cun total dunhas 700 páxinas, no ano 1967 descúbrense na Biblioteca Nacional de Madrid os documentos que serían coñecidos como Códice de Madrid I e II. O seu autor era Leonardo da Vinci (1452-1519). No folio 36-verso do tomo I atopamos un debuxo dun mecanismo de transmisión mediante un engranaxe no que a relación de transmisión é de 1:10. Por cada 10 voltas que lle deamos a unha roda, a seguinte moverase unha décima parte. Como segundo o esquema de Leonardo, a máquina consta de 13 unidades ensambladas, para que se mova un dente da última cómpre que que deamos 1.000.000.000.000 (un billón) de voltas á primeira roda. No seguinte vídeo vemos unha versión dixital deste aparato con 7 rodas no canto de 13.
 Ao pouco deste achádego o enxeñeiro Roberto A. Guatelli (1904-1993), experto mundial na obra de Leonardo da Vinci constrúe unha calculadora basándose no anterior esquema do Códice de Madrid I. Guatelli estaba especializado na construción de réplicas das máquinas de Leonardo, porén nesta ocasión ademais das indicacións do folio 36-verso Guatelli fai uso doutros mecanismos descritos tamén por da Vinci no Códice Atlántico pero que non eran da súa invención pois xa aparecían nun libro de Vitrubio do século I a. C. Con esta base constrúe unha calculadora para unha exposición da IBM que pretendía ser unha réplica do boceto de Leonardo pero á que se lle ven unha chea de defectos: nos comenzos do XVI non ten ningún sentido unha calculadora con tantas cifras; non hai ningunha marca numérica; tampouco se enxerga ningún mecanismo para introducir novos sumandos, o rozamento que se produciría sería tal que ao cabo dunhas poucas voltas resultaría imposible mover a maquinaria,....
Ao pouco deste achádego o enxeñeiro Roberto A. Guatelli (1904-1993), experto mundial na obra de Leonardo da Vinci constrúe unha calculadora basándose no anterior esquema do Códice de Madrid I. Guatelli estaba especializado na construción de réplicas das máquinas de Leonardo, porén nesta ocasión ademais das indicacións do folio 36-verso Guatelli fai uso doutros mecanismos descritos tamén por da Vinci no Códice Atlántico pero que non eran da súa invención pois xa aparecían nun libro de Vitrubio do século I a. C. Con esta base constrúe unha calculadora para unha exposición da IBM que pretendía ser unha réplica do boceto de Leonardo pero á que se lle ven unha chea de defectos: nos comenzos do XVI non ten ningún sentido unha calculadora con tantas cifras; non hai ningunha marca numérica; tampouco se enxerga ningún mecanismo para introducir novos sumandos, o rozamento que se produciría sería tal que ao cabo dunhas poucas voltas resultaría imposible mover a maquinaria,....O reloxo de Schickard
Por todo o exposto considérase que a primeira máquina de calcular foi construída no 1623 por Wilhelm Schickard (1692-1635) un astrónomo alemán. O seu reloxo de cálculo podía realizar as catro operacións básicas. Pero o único que se construiu foi destruído nun incendio no 1624 seguramente nun incendio provocado por alguén que non soportaba que a máquina fose quen de realizar as mesmas operacións que "un espíritu sagrado e inviolable" do ser humano. Velaquí unha reconstrucción do reloxo calculador de Schikard a partir dun esquema recollido dunha carta que lle enviou ao eminente astrónomo Kepler:
O maior defecto da pascalina era que non podía realizar produtos e divisións. Para superar esta limitación Gottfried Wilhelm Leibniz (1646-1716) , matemático, filósofo e diplomático alemán elabora unha máquina moito máis complexa que a de Pascal. Constrúe un exemplar no 1694 e outro no 1704, pero os seus mecanismos, demasiado complexos para o desenvolvemento tecnolóxico da época, nunca chegaron a funcionar satisfactoriamente. De todas formas, as innovacións que achegadas por Leibniz habían de ser utilizadas polos seguintes inventores.
O aritmómetro
Seguramente o deseño máis importante realizado sobre a base da calculadora de Leibniz sexa o aritmómetro. Esta calculadora ideada por Charles-Xavier Thomas de Colmar (1785-1870), un enxeñeiro francés que era director dunha compañía de seguros en París. A primeira versión foi contruída no 1822. Foi a primeira calculadora con éxito comercial de toda a historia, a súa produción estederase con sucesivas versións desta máquina durante todo o século XIX, incluso despois da morte de Thomas de Colmar, ata o ano 1915.
A multiplicadora de Ramón Verea.
Todas as caculadoras construídas ata o último cuarto do XIX tiñan un evidente incoveniente. Basaban o cálculo do produto nunha serie de sumas sucesivas. Ademais este procedemento non era automático. Todo isto cambiou coas aportacións que fixo Ramón Verea (1833-1899), cando no ano 1878 patentou en Nova York un mecanismo que podía realizar directamente multiplicacións cunha capacidade de obter resultados de ata quince cifras. Ramón Verea era plenamente consciente de cal fora a súa aportación á tecnoloxía das máquinas calculadoras. Nun artigo publicado no xornal Las Novedades de Nova York Verea afirmaba que
Non sei se algún dos inventores que me precederon soñou algunha vez cunha máquina de calcular; pero sei que todos os aparatos ata o de hoxe inventados non fan máis que contar,Por iso, aínda que puxera como desculpa que só pretendía reforzar o orgullo da súa orixe, resulta realmente estraño que non chegara a comercializar o seu invento. Outros si que o fixeron. É o caso de León Bollée, inventor do primeiro coche de gasolina, gañador no 1889 dunha medalla de ouro na Exposición Universal de París do 1889 por unha calculadora que realizaba rápidamente grandes produtos e divisións. No 1892 Otto Steiger, sobre a tecnoloxía desenvolvida por Bollée e Verea construirá un modelo que sería todo un éxito comercial: a millonaria.
Para saber máis:
The history of computing project
arithmometre.org
History of computers Rechnerlexikon. Die große Enzyklopädie des mechanischen Rechnens
Códice de Madrid
Storia d´ell informatica, pdf didáctico
Ramón Verea. Inventor estradense, libro de Olimpio Arca Caldas
Historia universal de las cifras, libro de Georges Ifrah, editado por Espasa
Etiquetas:
#cienciaengalego,
calculadora,
Charles-Xavier Thomas de Colmar,
Día da Ciencia en Galego,
historia,
Leonardo da Vinci,
Pascal,
Ramón Verea,
Roberto A. Guatelli,
Schickard,
tecnoloxía,
TIC,
vídeo
sábado, 3 de novembro de 2012
Simetría, enigma da realidade
Despois da anterior entrada, cunha curta biográfica de Galois, pareceume unha boa forma de continuar comenzar coa súa morte nun duelo a principios do XIX, que non é máis que a forma, orixinal e espectacular, coa que o divulgador Marcus du Sautoy, comenza esta conferencia encol da simetría, unha das principais claves das matemáticas no comenzo dos XXI.
Quen queira ampliar esta conferencia pode consultar esta outra, impartida en Barcelona no 2009, na que debulla os mesmos tópicos que no seu libro Simetría.
Recursos sobre Ramón Verea e a súa calculadora
 No ano 2010 realizáronse unhas xornadas de divulgación da figura de Ramón Silvestre Verea García n´A Estrada. A Asociación Cultural Vagalumes gravou algunha das conferencias impartidas. Para que a lembranza de Ramón Verea perdurase encargouse unha escultura da que deixamos aquí unha imaxe recollida da Galipedia. Tamén se presentou unha biografía, que vén sendo o mellor material para achegármonos á figura deste inventor e periodista da segunda metade do XIX.
Xunto con todo este material hai moitos outros máis recursos que nos achegan ao perfil dun librepensador que foi quen de inventar unha máquina que por primeira vez na historia podía facer produtos sen ter que realizar unha serie de sumas sucesivas.
No ano 2010 realizáronse unhas xornadas de divulgación da figura de Ramón Silvestre Verea García n´A Estrada. A Asociación Cultural Vagalumes gravou algunha das conferencias impartidas. Para que a lembranza de Ramón Verea perdurase encargouse unha escultura da que deixamos aquí unha imaxe recollida da Galipedia. Tamén se presentou unha biografía, que vén sendo o mellor material para achegármonos á figura deste inventor e periodista da segunda metade do XIX.
Xunto con todo este material hai moitos outros máis recursos que nos achegan ao perfil dun librepensador que foi quen de inventar unha máquina que por primeira vez na historia podía facer produtos sen ter que realizar unha serie de sumas sucesivas.
- Ramón Verea. Inventor estradense, libro de Olimpio Arca Caldas. Editado por galeguizargalicia.com. Descargar o pdf
- Ramón Verea García por Olimpio Arca Caldas, vídeo da A. C. Vagalumes coa conferencia impartida polo mestre Olimpio Arca no Recreo Cultural d´A Estrada o 23 de abril de 2010
- Ramón Verea García en Curantes, vídeo da A. C. Vagalumes coa conferencia impartida polo historiador Ricardo Gurriarán
- Ramón Silvestre Verea, traballo do escultor Molares, por encargo do Foro Enrique Peinador e o Concello da Estrada, para a homenaxe do escritor e inventor de Curantes.
- Ramón Verea, entrada na Galipedia
- Biography of Ramón Verea, artigo sobre a vida de History of Computers
- Ramón Verea, artigo sobre a calculadora de Verea en History of Computers
- Ramón Verea: o inventor da primeira calculadora, artigo en Galicia espallada
- Ano Cultural na Estrada – Ramon Verea?, post no blogue belay.es
- Patente da calculadora de Ramón Verea, descargar o pdf ou ver en liña
- La primera calculadora que multiplicaba, programa tres14 de RTVE
- Los vecinos de Curantes pretenden reuperar la figura de Ramón Verea, artigo en El Correo Gallego o 19/04/2009
- La aritmética y los principios, artigo en El País 04/08/2013
- Ramón Verea García: inventor, librepensador e galego universal, na Enciclopedia da Emigración Galega, elaborada por CIG-emigración
- Ramón Verea. O librepensador que inventou a primeira calculadora, neste mesmo blogue
- Ramón Verea, inventor. Presentación do blogue Lingua de Montes
- Verea Direct Multiplier, referencia da calculadora multiplicadora de Verea no museo da IBM. Neste apartado 'Antique artefacts' ([1], [2] e [3]) podemos situar históricamente o invento de Verea.
- Timeline of computing hardware 2400 BC–1949, liña de temporal na que situar o invento de Verea, da Wikipedia
mércores, 31 de outubro de 2012
Ramón Verea. O librepensador que inventou a primeira calculadora
No que hoxe é a parroquia estradense de San Miguel de Curantes nacía o 11/12/1833 Ramón Silvestre Verea García, fillo de Juan Verea Filloy e Florentina García Porto, "pobres, pero de respectado abolengo" segundo informa un amigo de Ramón Verea.
No ano 1845 chega a Santiago para estudar. Ingresa no Seminario no 1848 e recibe clases de teoloxía. Xa desencantado coa Igrexa, e logo dun desencontro co rector e o arcebispo abandona no 1854 a formación eclesiástica. O historiador da USC Ricardo Gurriarán aventura que posiblemente Verea tivo contacto coa Sociedade Económica de Amigos do País ou co Ateneo Popular e alí recibiría formación en ámbitos alonxados da escolástica.
Aos 22 anos, estamos no 1855, marcha a Cuba sen ningún tipo de protección nin título universitario que lle facilite abrirse camiño nunha terra descoñecida. Exerce de mestre en escolas dos campos cubanos. Pero pronto inicia a actividade que lle ocupará a maior parte da súa vida: o periodismo. Comenza publicando artigos nun xornal, El Progreso, editado na cidade cubana de Colón e que dirixiría a partir do 1862. Alí publica duas novelas: La Cruz de Piedra e Una mujer con dos maridos.
No ano 1865 marcha a Nova York onde vende os dereitos dun invento seu a un especulador. Tratábase dun dobrador de xornais. Dous anos despois volve a Cuba co proxecto de crear unha empresa de maquinaria . O proxecto non obtivo o éxito que Verea imaxinaba. Ao cabo de dous anos establécese en Nova York onde exerce de profesor de español, tradutor público, corresponsal científico dun xornal, ou mesmo de comerciante. Obtén un bo capital e no 1875 establece unha "Axencia industrial para a compra de maquinaria e efectos de moderna invención".
É no 1878 cando patenta a súa máquina de cálculo que recibiría a medalla de ouro dunha exposición en Matanzas (Cuba). O propio Verea é consciente da importancia do seu invento. El mesmo explica que as máquinas construídas ata o momento facían sumas engadindo unha cantidade sobre outra, isto é, limitábanse a contar. Pola contra o artefacto de Verea era unha máquina que calculaba. Así, ademais de sumas e restas podía realizar produtos e divisións facilitando resultados de ata quince cifras cun factor de nove cifras e outro de seis.
Embarca para Galicia no 1879. Volve a Nova York dous anos despois. Durante un tempo traballa como redactor do xornal El Cronista do que chega incluso a exercer de director. Faise coa propiedade dunha imprenta e funda e dirixe unha revista quincenal: El Progreso. Este xornal non ten publicidade e substentaríase grazas a unha estensa rede de subscritores por todo o mundo. Edita ademais dous folletos (Catecismo librepensador ó cartas a un campesino e Contra el altar y el trono) e un libro (La religión universal ) nos que defende incisivamente as súas ideas.
Os negocios comenzaron a irlle mal, así que farto do utilitarismo imperante en Nova York, e buscando un lugar de clima máis benigno para os seus problemas de saúde abandona definitivamente a cidade norteamericana no ano 1895 con destino a Guatemala onde é recibido moi agarimosamente polo presidente Reina-Barros. Non tarda en entrar en conflito con altos cargos do goberno guatemalteco. Os puntos de descordo estaban relacionados coa interpretación da historia e da política hispanoamericana.
Buscando un lugar onde as súas ideas fosen mellor acollidas marcha de Guatemala no 1897, desta vez con destino a Arxentina onde tiña algúns familiares. En Buenos Aires volve a poñer en marcha un xornal, tamén coa cabeceira de El Progreso. Nesta nova edición chega a publicar 164 números pero por mor dunha infección pulmonar Ramón Verea morre só dous anos despois da súa chegada á capital arxentina.
Nunca deixou de ter relación con Galicia pois o mesmo ano da súa morte 1899, o xornal compostelano Gaceta de Galicia daba a noticia de que Ramón Verea donara á Universidade de Santiago dous tomos coa revista que publicaba en Nova York.
Ao seu enterro asistiron dúas ducias de persoas entre as que destacaban personalidades do partido socialista arxentino. Os seus restos xacen no cemiterio bonaerense do Oeste nunha tumba sen lápida.
Un librepensador
Verea cualificábase a si mesmo como un librepensador. Non se ten coñecemento de onde parten as súas ideas sociais e políticas. Nas notas biográficas que se lle fixeron establécese como un feito que había de influirlle moito: a execución en Carral dos sublevados contra o goberno de Narváez que reivindicaban un trato máis xusto para Galicia e a restauración das liberdades abolidas. O historiador da USC Ricardo Gurriarán apunta a que posiblemente recibiu formación na Sociedade Económica de Amigos do País ou co Ateneo Popular e alí entraría en contacto con ideas alonxadas da escolástica. As ideas políticas de Ramón Verea están tinxidas de republicanismo:
Non pode ser casualidade que cada vez que fundaba un xornal a súa cabeceira fose sempre El Progreso. Ramón Verea confiaba no desenvolvemento da sociedade por medio do avance na tecnoloxía , aseguraba que o futuro viría por este camiño e laiábase de que se ensinara únicamente
Verea cualificábase a si mesmo como un librepensador. Non se ten coñecemento de onde parten as súas ideas sociais e políticas. Nas notas biográficas que se lle fixeron establécese como un feito que había de influirlle moito: a execución en Carral dos sublevados contra o goberno de Narváez que reivindicaban un trato máis xusto para Galicia e a restauración das liberdades abolidas. O historiador da USC Ricardo Gurriarán apunta a que posiblemente recibiu formación na Sociedade Económica de Amigos do País ou co Ateneo Popular e alí entraría en contacto con ideas alonxadas da escolástica. As ideas políticas de Ramón Verea están tinxidas de republicanismo:
"O Rei pasou de moda nos países civilizados. Conserva o nome, pero foi despoxado das bárbaras facultades que asumira [...]. O poder que antes se supoñía vir de arriba, descubiruse agora que vén de abaixo. As árbores non están prendidas á atmosfera polas pólas; estano á terra polas raíces"Tamén foi un firme defensor dos máis desfavorecidos. Nun seu artigo do que dá conta Waldo Álvarez Insua, denuncia que non se condene a un policía por asesinato dun mariñeiro galego. Moitas veces a súa crítica social vóvese en crítica política:
"Pesoume a morte deses compatriotas meus que traballan toda a vida, famentos e espidos, que viven en chozas que non serven para animais, e todo isto para manter na folganza un exército de gobernantes e pretendentes"Dóelle que os gobernos actúen como opresores dun pobo ao que utilizan e esquilman para manter unhas estruturas de goberno atrasadas. Usa a súa voz para denunciar as inxustizas sociais e ataca o trato que o poder mantén cos que teñen menos recursos. Encol dos campesiños di que
"Cando os seus fillos son crecidos e poderían axulado, arrebátanllos para o servizo das armas, onde van ser sacrificados, tal vez por un principio político que el non entende ou non lle importa, e en todo evento para apoiar ao goberno que o oprime. Antes de comer ten que pagar as contribucións á Igrexa e ao Goberno. Se non lle chega, élle forzoso empeñar as súas terras ou polo menos, o produto das súas futuras colleitas, en mans dalgún usureiro"Un exemplo mala xestión procedente de Europa, en concreto de España, é para Verea o caso de Cuba, "levamos a Illa ás portas da bancarrota e da miseria". Pola contra é moi belixerante cos movementos pola independencia pois consideraba que se Cuba chegara a romper os vecellos coa metrópoli sería para caer nas gadoupas doutra potencia, posiblemente os Estados Unidos. Verea identifica a Europa co atraso e xustifica que moita xente queira fuxir do vello continente para fuxir da miseria ou librarse dunhas levas que recollen o mellor do sangue social para devolver un zume inútil cando se xa se lle sacaron os mellores produtos para utilizalos en guerras ou campañas sen xustificación algunha.
Para que serven eses millóns de homes que compoñes os exércitos permanentes, máis que para soster autócratas e defendelos dos seus mesmos pobos?Dadas as circunstancias sociais, a extrema pobreza xustificaría que se promovese a emigración pois "neste caso non é obra de utilidade soamente: éo de humanidade". Pon como exemplo o edificio "Castle Garden" de Nova York onde empregados estatais e tradutores orientan aos inmigrantes como un caso de boa política de acollida que pode facerlle frente aos malvados que queren aproveitarse dos estranxeiros. Ramón Verea chega a ir moito máis alá ao opinar sobre o problema da emigración, problema que el ve como unha oportunidade chea de ventaxas:
"Cantos máis sexan os que se ausente, mellor estarán os que queden, porte faltando brazos será mellor remunerado o traballo"O estradense ve en América as potencialidades do progreso. Trátase dun continente por construir e que pode ser levantado polos emigrantes procedentes de Europa. En América aínda son posibles os ideais de liberdade e avance. Un dos aspectos nos que destaca como adiantado ás ideas imperantes na súa época é no da defensa da igualdade para a muller:
"Mentres o home se considere o amo da muller, mentres lle negue a igualdade civil, menres non a mida coa mesma vara que a si mesmo, non poderá dicir con verdade que dou un paso no sendeiro do verdadeiro progreso"Probablemente a bandeira da defensa das mulleres recóllea despois de romper coas forma tradicionais de poder simbolizadas polo altar e o trono (El altar y el trono é tamén o título dun dos seus libros). Do segundo xa falamos máis arriba. No relativo ás súas discrepancias coa Igrexa sabemos que xa as comenzara a dixerir estando no Seminario pois cando o abandona declara sentirse aliviado.
"Estudei a teoloxía e vin que era un castelo de naipes; que non resistía nin o máis leve sopro da razón"Usa reiteradamente un argumento que revela o seu carácter humanista, superador dos chauvinismos. Consideremos que nacemos noutro lugar, entón no canto de crer fervorosamente no noso deus, serímos xudeos, musulmáns,... en consideraríamos por simple filiación estarmos en posesión da única verdade. Non ten sentido a idea dun deus que non incrustara en toda a humanidade a luz da fe, cunha claridade total semellante á que inspira as verdades matemáticas, agás que ese deus sexa un ser cruel:
"Os que eninan que fóra da verdadeira relixión non hai salvación, non teñen entrañas nin llas supoñen a Deus. Se o mundo fose creado por un xenio infinitamente malo, explicaríase que fose imposible distinguir a relixión verdadeira das falsas, porque era o xeito de perder ao home; pero o que fixo o aire para o pulmón e aluz para a vista non podía, sen deixar de ser quen é, ocultar o aire e a luz da via espirtual"Así considera ás relixións como "as maiores pragas da humanidade". É especialmente crítico coa venda do perdón dos pecados, o cobro da impartición dos sacramentos,...en definitiva o abuso de poder da Igrexa
"A idea de Deus foi enxendrada polo medo, e as relixións positivas son enxendros da codida, alimentadas pola ignorancia"A máquina de calcular
Non pode ser casualidade que cada vez que fundaba un xornal a súa cabeceira fose sempre El Progreso. Ramón Verea confiaba no desenvolvemento da sociedade por medio do avance na tecnoloxía , aseguraba que o futuro viría por este camiño e laiábase de que se ensinara únicamente
"filosofía, ciencias, literatura. Temos sobrados médicos e avogados, algúns pintores e moitísimos literatos e poetas. Os enxeñeiros son moi escasos e educados case todos en países estranxeiros"Nesta mesma liña propugna o ensino da mecánica desde a secundaria. En coherencia con estas ideas establece dicotomías entre o progreso e o atraso:
"O deber fórzanos a censurar aos mexicanos, país onde case todos os progresos son importados, aplicouse a luz eléctrica ás corridas de touros. Se ese adianto moderno non poidese ter mellor aplicación, prefiriríamos que se suprimise"Despois de moitos esforzos e de dous intentos fracasados Ramón Verea consigue fabricar o que el mesmo cualifica como primeira máquina de calcular. Para alcanzar este obxectivo comenzara estudando a historia das máquinas aritméticas. Fai referencia á inventada por Pascal, a coñecida como Pascalina e presentada no 1642, tiña un mecanismo que só lle permitía facer sumas e restas. O invento de Leibniz, aínda que realizaba tamén produtos e divisións, nunca chegara a funcionar correctamente ata que a reloxería avanzou o suficiente Charles-Xavier Thomas de Colmar, director dunha compañía de seguros en París, inventara o seu aritmómetro mellorando o deseño de Leibniz, unha máquina da que fabricaría diferentes versións. Todas as máquinas aritméticas inventadas ata o 1878 partillaban un inconveniente pois os produtos efectuábanse con procedementos non automáticos. As multiplicacións obtíñanse por medio de adicións sucesivas. Verea explicaba isto moi claramente diferenciando entre os procesos de contar versus o de calcular:
Se nos dan seis montóns con sete grans cada un e imos contando 1, 2, 3,..., 40, 41, 42, entón contamos: pero se decimos 7x6 = 42, facemos un cálculo en pequena escala. É verdade que contando podemos chegar ao mesmo resultado que calculando; por exemplo 6.729.465 x 38.976 podemos pescudar o resultado sumando o primeiro factor 38.976 veces, ou viceversa; pero, canto máis breve e simple non é facer a multiplicación? O primeiro fano as máquinas coñecidas, o segundo só o fai a miña.[...] Aquilo é contar, isto é calcular.Sendo fieis ao sentido destas palabras, a máquina de Ramón Verea foi propiamente a primeira calculadora. Desafortunadamente o invento non chegou a comercializarse. Se atendemos ás súas declaracións foi porque o seu interese non residía nos cartos ou na celebridade que podía adquirir coa venda da calculadora, senón que o seu empeño era o de contribuir ao avance da ciencia e o de demostrar que a pesar da súa orixe era tan capaz na inventiva e na imaxinación como como un oriundo dunha nación culta. Despois de dous intentos sen éxito, o terceiro modelo,cun peso de 22 kg, funcionaba sen problemas. Tiña unha capacidade operativa para nove cifras no sumando, multiplicando ou divisor e para seis no multiplicador ou cociente. En consecuencia podíanse obter resultados de ata quince cifras. As súas dimensións en centímetros son de 36x30x20 cm. Para saber máis: ARCA CALDAS, Olimpio, Ramón Verea. Inventor estradense. Editado por galeguizargalicia.com
domingo, 28 de outubro de 2012
A máquina de calcular, por Ramón Verea
No número XVIII de La Ilustración Gallega y Asturiana, publicado en Madrid o 28 de xuño do 1881 é noticia a unha nova máquina de calcular creada por "un inventor galego". Tratábase de Ramón Verea. Nese mesmo número reprodúcese un artigo de Verea aparecido no xornal Las Novedades de Nova York que reproducimos aquí. Nel o inventor explica con moita claridade o significado da súa aportación.
As características principais da calculadora xa as explicara así: "A máquina que teño é a terceira que fixen: a súa capacidade é para nove cifras no sumando, multiplicando ou divisor, seis no multiplicador ou cociente, e quince no produto ou dividendo" e pasa a dar as súas dimensións: 36x30x20 cm.
É impresionante a lucidez con que Verea nos explica a importancia do seu invento:
Das numerosas invencións hoxe coñecidas, non hai unha soa na que fracasaran tantos e tan eminentes xenios como na máquina de calcular. Entre outros moitos, os nomes de Pascal e Leibniz, tan célebres no mundo das ciencias exactas son testemuña deste, polo que parece, atrevido aserto. Antes de ir máis lonxe debo facer notar a diferenza esencial que existe entre as máquinas de contar e as de calcular para demostrar que o terreo relativamente facil no que traballaron os inventores das primeiras e as dificultades coas que loitou o que subscribe para substituir un mecanismo que calcule, palabras que a primeira vista se rexeitan, e que parece imposible dixerilas xuntas. Non sei se algún dos inventores que me precederon soñou algunha vez cunha máquina de calcular; pero sei que todos os aparatos ata o de hoxe inventados non fan máis que contar, pois o seu alcance non fai máis que sumar e restar, operacións que nada teñen de cálculo. Se nos dan seis montóns con sete grans cada un e imos contando 1, 2, 3,..., 40, 41, 42, entón contamos: pero se decimos 7x6 = 42, facemos un cálculo en pequena escala. É verdade que contando podemos chegar ao mesmo resultado que calculando; por exemplo 6.729.465 x 38.976 podemos pescudar o resultado sumando o primeiro factor 38.976 veces, ou viceversa; pero, canto máis breve e simple non é facer a multiplicación? O primeiro fano as máquinas coñecidas, o segundo só o fai a miña. Para pescudar cantas son nove veces nove, contan nove, dez, once, etc., ata oitenta e unha. Eu saco o resultado a un golpe facendo aparecer simultanemente 8 nunha roda e 1 na que lle segue á dereita; e se no canto de 9x9 poñemos 846.728.235x9, o produto de cada cifra do multiplicando aparecerá a un tempo, formando o total completo. As primeiras, á maneira da materia non poden ir dun punto a outro sen pasar polos puntos intermedios; a segunda, como o espíritu pasa dos factores ao produto como se entre éstes non mediara distancia ningunha. Aquilo é contar, isto é calcular. Por ser precisamente tan mal aritmético, pensei nunha máquina que fixese máis ca min: que non se equivocase. Con este pensamento púxenme a estudar a historia da invención, e o que a outro o faría desistir do proxecto, a min animoume: Parecíame por unha parte excesiva presunción acometer unha empresa onde homes tan grandes sucumbiran; pero, por outra parte, seducíame a idea de deixar atrás esa falanxe de celebridades. Tiña as miñas presuncións de mecánico e inventor: e onde probalas mellor que nunha máquina de calcular? Cábeme a satisfación de dicir que de nada me serviron os traballos dos que me precederon. Non mellorei ningunha das máquinas existentes: inventei unha enteiramente nova no principio fundamental e nos seus detalles máis esenciais. Ata aquí fixéronse máquinas para substituir as mans do home, para facer traballos mecánicos; pero ningunha para executar os traballos puramente intelectuais; nunca unha combinación de pezas metálicas substituíra ao entendemento; nunha a máquina competira, nin tan siquera igualara, ao espíritu en rapidez Coñezo os principios da mecánica; teño unha idea dos mecanismos máis difíciles; pero non souben nunca dunha máquina que encerrara tantas dificultades O meu obxecto ao emprender unha invención a primeira vista imposible non foi a esperanza de reembolsar xamais nin unha parte dos vaios miles de pesos que gastei; nin será tampouco coa celebridade qeu outros por menos adquiriron, e que eu non ambicionei; os meus móbiles foron: 1) un pouco de amor propio; 2) moito de amor nacional, o desexo de probar que en xenio inventivo un español pode deixar atrás ás eminencias das nacións máis cultas; 3) o afán de contribuir con algo ao adianto da ciencia; e 4) o último, un entretemento conforme aos meus gostos e inclinacións
xoves, 25 de outubro de 2012
Evariste Galois. Curta do 1965
Curta do ano 1965 que foi premiada no festival de Cannes. dirixida por Alexandre Astruc, periodista e director de cine francés. AstrucTamén publicou un libro sobre o matemático francés.
Galois naceu un día coma hoxe, 25 de outubro, no ano 1811.
mércores, 24 de outubro de 2012
Mini-documental sobre Ramón Verea na TVE
tres14 - La primera calculadora que multiplicaba
O III Día da Ciencia en Galego, xornada que reivindica a derrogación do funesto decreto 79/2010 que intenta erradicar o uso do galego do ámbito científico, está adicado a Leonardo da Vinci e Ramón Verea.
Grazas aos compañeiros de Lalín, desde A Marela Tarabela, enterámonos deste documental do programa tres14 da TVE que nos relata a importante aportación deste galego, Ramón Verea, á historia da tecnoloxía do cálculo coa invención da primeira máquina que multiplicaba.
O III Día da Ciencia en Galego, xornada que reivindica a derrogación do funesto decreto 79/2010 que intenta erradicar o uso do galego do ámbito científico, está adicado a Leonardo da Vinci e Ramón Verea.
xoves, 27 de setembro de 2012
Así é imposible ser millonario
A cuestión, de artimética infantil, nin tan siquera require que pensemos na resposta exacta. De todas formas a concursante demostra o seu analfabetismo matemático.
O seguinte caso ten algo máis de voltas e se o concursante non estaba un pouco avisado podía meter a zoca. Non se pregunta sobre cal dos números é o menor cadrado. A cuestión é saber cal destes catro cadrados:
a:16 b:25 c:36 d:49
é tamén a suma dos cadrados máis pequenos. Para responder cómpre lembrar o que son as ternas pitagóricas: coleccións de tres números enteiros que verifican o Teorema de Pitágoras. Dito doutro xeito, temos que pensar en tres números de forma que o cadrado dun deles é igual á suma dos cadrados dos outros dous. Velaquí algunhas desas ternas:
(3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41),
(11, 60, 61), (12, 35, 37), (13, 84, 85), (16, 63, 65), (20, 21, 29)
Con estes datos diante non nos sería difícil conseguir 15.000 $.
Vía Clube da Matemática e Zenbakiak
O seguinte caso ten algo máis de voltas e se o concursante non estaba un pouco avisado podía meter a zoca. Non se pregunta sobre cal dos números é o menor cadrado. A cuestión é saber cal destes catro cadrados:
a:16 b:25 c:36 d:49
é tamén a suma dos cadrados máis pequenos. Para responder cómpre lembrar o que son as ternas pitagóricas: coleccións de tres números enteiros que verifican o Teorema de Pitágoras. Dito doutro xeito, temos que pensar en tres números de forma que o cadrado dun deles é igual á suma dos cadrados dos outros dous. Velaquí algunhas desas ternas:
(3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41),
(11, 60, 61), (12, 35, 37), (13, 84, 85), (16, 63, 65), (20, 21, 29)
Con estes datos diante non nos sería difícil conseguir 15.000 $.
Vía Clube da Matemática e Zenbakiak
mércores, 19 de setembro de 2012
Detritus
Nesta animación experimental debuxada a lápiz, e recuperada dunha copia en VHS, aparecen diversas figuras xeométricas. Entre elas vemos unha conexión entre os vértices dun rectángulo mediante segmentos que vén sendo o camiño máis curto que podemos trazar entre eles.
Vía puntoyrayafestival
xoves, 13 de setembro de 2012
Chámalle "xe". Invitación ás matemáticas en galego.
A Comisión de Normalización Lingüística da Facultade de Matemáticas da USC escolleron o lema Chámalle "xe" para promover o uso do galego no esotérico mundo das matemáticas. Pero fixeron máis.
Redactaron un texto que non sería outra cousa que unha invitación inxenua ao uso do galego a aqueles universitarios que, nun futuro, desenvolvan a súa vida profesional en Galicia. Pero é tal o estado de cousas na política lingüística do actual goberno da Xunta, que facer esta morna indicación é unha chamada ao incumprimento do aldraxante decreto 79/2010, o publicitado como o do plurilingüismo e que prohíbe a impartición das clases de matemáticas en galego.
Agora que vai dar comenzo o curso nas aulas de secundaria, convén que os profesores que estudáchedes matemáticas na USC poñades atención e, se aprendíchedes algo, que sexa polo menos isto.
Velaquí o texto da CNL da Facultade de Matemáticas:
As matemáticas contan coa súa propia linguaxe, a linguaxe matemática. Comprendela e saber utilizala é unha das competencias que debedes adquirir nos estudos do grao en Matemáticas. Xunta esta habedes conseguir outra: comunicar, tanto por escrito como de forma oral, coñecementos, procedementos, resultados e ideas en matemáticas tanto a un público especializado como non especializado. Daquela, non só comprenderedes o que é senón que seredes quen de comunicárllelo a outras persoas. E para iso utilizaredes linguas naturais; calquera delas, a que mellor se adapte ao voso interlocutor; e que vós coñezades, naturalmente. Moitos de vós -probablemente, a maioría- atoparedes en Galicia a vosa saída profesional. Outros sairedes ao exterior. Debedes contar coa mellor preparación posible. Aprendede linguas. Mais seguide aprendendo e cultivando tamén a lingua deste país, o galego, para poderdes trasladarlles a beleza das matemáticas aos galegos e galegas.
mércores, 12 de setembro de 2012
Máis alá do infinito
Podemos comprobar neste exemplo que se pode escribir un disparate científico coma este, que non pasa nada. Resulta que a Voyager 1 se está aproximando ao infinito, un lugar que segunda a mesma noticia debe andar polos 18.000 millóns de km de distancia. Concretamente 18.236.222.780 km no momento en que eu o mirei, ou se o preferimos, 121,90161996 Unidades Astronómicas (Que é unha unidade astronómica?, simplemente a distancia media entre a Terra e o Sol, aproximadamente 149.597.870 km.). Podemos consultar esas distancias nesta páxina da NASA.
Supoño que o intre no que no Voyager 1 alcance o infito será un fito histórico a destacar para a humanidade. Despois diso a tecnoloxía non terá máis cara onde avanzar. Estaremos atentos.
venres, 7 de setembro de 2012
Aperitivos de poliedros platónicos
Curiosa e divertida forma de conxugar gastronomía e matemáticas. Do web de Francesc Forcada.
Vía Amazings.es
luns, 3 de setembro de 2012
venres, 31 de agosto de 2012
Curiosity chega a Marte
Retransmisión da 'amartizaxe' da Curiosity na linguaxe típica dos eventos deportivos. Moito máis emocionante ca éstes últimos.
mércores, 8 de agosto de 2012
A calculadora de Ramón Verea
Como profesor de matemáticas, en moitas ocasións teño que explicar o funcionamento de determinadas funcións dunha calculadora. Neses casos non podo deixar de lembrar a figura de Ramón Verea. Como teño a certeza de que é un descoñecido vou deixar aquí algúns apuntes sobre quen foi ese home.
Nun acto celebrado en novembro do 2009 e organizado polo Foro Enrique Peinador ([1], [2]), homenaxeouse a Ramón Silvestre Verea García, natural da parroquia de Curantes (A Estrada) do que se destacaba o mérito de ser o inventor da calculadora. Despois do descubrimento dun busto realizado polo escultor Manuel Molares interveñen o historiador Ricardo Gurriarán e o mestre Olimpio Arca Caldas, autor do libro Ramón Verea.
Para sermos máis precisos convén matizar o título que se lle asigna en moitos lugares a Ramón Verea como o de ser o inventor da calculadora. Non hai ningunha persoa á que se lle poida atribuir en exclusiva este invento. Os precursores xurdiron no XVII. Un deles foi o reloxo calculador de Wilhem Schikcard,, outros foron os artefactos dos ilustres matemáticos Leibniz e Pascal: a máquina artimética do primeiro e a pascalina do segundo. No XIX patentaríanse moitas máquinas de calcular e faríanse importantes aportacións ao desenvolvemento da tecnoloxía do cálculo. Unha delas viría de Ramón Verea. Concretamente o seu invento, patentado no 1878 ten o mérito de poder realizar produtos directamente pois ata o momento realizábanse mediante unha repetición de sumas. Segundo as palabras do propio Verea:
A miña máquina, ademais de sumar e restar, multiplica e divide polo sistema abreviado que usamos, coa vantaxe de multiplicar todo o multiplicando á vez por cada número do multiplicadorReivindicar a este noso veciño é tamén reafirmarse no orgullo do propio, do noso. Ramón Verea, un veciño da parroquia estradense de Curantes, mestre e redactor dun xornal, director doutro, escritor, tradutor, inventor e empresario, actividades que realiza en Cuba, Estados Unidos, Guatemala e finalmente Arxentina, onde morre no 1899. Se un profesor de matemáticas coma min, quixera aproveitar a figura e a proximidade de Verea para facer agromar ese orgullo aparellado á reafirmación da lingua de noso, tería un serio problema pois para facelo deberá enfrentarse aos ditames da Consellería de Educación. Creo que non hai que volver a recordar os funestos mandatos do decreto 79/20120, o chamado decreto do plurilingüismo que prohíbe, entre outras, as clases de matemáticas en galego. E aínda Valentín García, o secretario xeral de política lingüística é quen de dicir que os decretos non son importantes. Pois na súa mesma lóxica tampouco importará cambiar un por outro e por comenzar a facer algo (non se sabe de nada que fixera ata o día de hoxe), Valentín García, que asistiu ás xornadas corr
luns, 9 de xullo de 2012
Por que 'x' representa o descoñecido
Quero partillar este vídeo no que se explica por que o 'x' representa o descoñecido. Velaí que a culpa é do español.
xoves, 24 de maio de 2012
O número π e o decreto de plurilingüismo
O número  vale 3.2
vale 3.2
 Indiana librouse. Pola contra Galicia pode ser posta en ridículo por incluir nas letras dun DOG unha aberración estatística. No funesto decreto 79/2010, o do plurilingüismo sentenciase un kafkiano procedemento de recollida de datos como a disculpa fundamental para cambiar o marco legal do uso das linguas no ensino non universitario. Trátase da polémica 'Consulta ás familias' realizada en xuño do 2009, que no seu día foi moi cuestionada polo seu alto custo, 296.000 €. Calquera que teña un mímimo de idea dos fundamentos da estatística sabe que unha mostra de gran tamaño non ten por que ofrecer mellores resultados que outras con menos elementos. O que sí é fundamental é a boa escolla da mostra. Isto asegúrase con técnicas de mostraxe científicas. O proceso seguido neste caso, e sentenciado polo decreto 79/2010, é un exemplo perfecto do que non se debe facer.
Se realmeante se quixera saber cal era o estado de opinión sobre a linguas a empregar no ensino, bastaría con facer unha enquisa a unha mostra verdadeiramente representativa. Pola contra, Anxo Lorenzo quixo xogar a facer estatísticas e argallou unha monstruosidade científica. Vexamos.
A cuestión era obter información sobre as familias dos estudantes no ensino non universitario. Pouco hai que reflexionar sobre a poboación a estudar para concluir que é imposible unha recollida de datos con garantías. No canto de enviar un cuestionario a cada elemento da poboación, ou de escoller unha mostra representativa, tal e como se fai habitualmente nos estudos estatísticos:
Indiana librouse. Pola contra Galicia pode ser posta en ridículo por incluir nas letras dun DOG unha aberración estatística. No funesto decreto 79/2010, o do plurilingüismo sentenciase un kafkiano procedemento de recollida de datos como a disculpa fundamental para cambiar o marco legal do uso das linguas no ensino non universitario. Trátase da polémica 'Consulta ás familias' realizada en xuño do 2009, que no seu día foi moi cuestionada polo seu alto custo, 296.000 €. Calquera que teña un mímimo de idea dos fundamentos da estatística sabe que unha mostra de gran tamaño non ten por que ofrecer mellores resultados que outras con menos elementos. O que sí é fundamental é a boa escolla da mostra. Isto asegúrase con técnicas de mostraxe científicas. O proceso seguido neste caso, e sentenciado polo decreto 79/2010, é un exemplo perfecto do que non se debe facer.
Se realmeante se quixera saber cal era o estado de opinión sobre a linguas a empregar no ensino, bastaría con facer unha enquisa a unha mostra verdadeiramente representativa. Pola contra, Anxo Lorenzo quixo xogar a facer estatísticas e argallou unha monstruosidade científica. Vexamos.
A cuestión era obter información sobre as familias dos estudantes no ensino non universitario. Pouco hai que reflexionar sobre a poboación a estudar para concluir que é imposible unha recollida de datos con garantías. No canto de enviar un cuestionario a cada elemento da poboación, ou de escoller unha mostra representativa, tal e como se fai habitualmente nos estudos estatísticos:
Pouco lle faltou ao estado estadounidense de Indiana para ser mofa dos historiadores e matemáticos cando a finais do XIX estivo a punto de aprobar unha lei que determinaba que o número  era 3.2. O texto fora redactado por Edward Johnson Goodwin, un físico que convenceu a un membro do Parlamento estatal para que levara á Cámara de Representantes de Indiana unha lei establecendo ese curioso valor para o número
era 3.2. O texto fora redactado por Edward Johnson Goodwin, un físico que convenceu a un membro do Parlamento estatal para que levara á Cámara de Representantes de Indiana unha lei establecendo ese curioso valor para o número  . O texto foi aprobado en dous comités e proposto para a súa aprobación como lei no ano 1887. Porén un profesor de matemáticas e latín, Clarence Abiathar Waldo, ficou horrorizado ao enterarse da proposta polo que lle explicou aos senadores o disparate que estaban a punto de cometer. Finalmente os representantes fixéronlle caso a Waldo e a lei non cheou a aprobarse. En efecto, o número
. O texto foi aprobado en dous comités e proposto para a súa aprobación como lei no ano 1887. Porén un profesor de matemáticas e latín, Clarence Abiathar Waldo, ficou horrorizado ao enterarse da proposta polo que lle explicou aos senadores o disparate que estaban a punto de cometer. Finalmente os representantes fixéronlle caso a Waldo e a lei non cheou a aprobarse. En efecto, o número  é un número irracional: ten infinitas cifras decimais que non se repiten periódicamente. Incluso máis,
é un número irracional: ten infinitas cifras decimais que non se repiten periódicamente. Incluso máis,  é un número trascendente. Isto significa que non é solución de ningunha ecuación alxébrica con coeficientes enteiros.
é un número trascendente. Isto significa que non é solución de ningunha ecuación alxébrica con coeficientes enteiros.
Decrétase unha aberración estatística.
 Indiana librouse. Pola contra Galicia pode ser posta en ridículo por incluir nas letras dun DOG unha aberración estatística. No funesto decreto 79/2010, o do plurilingüismo sentenciase un kafkiano procedemento de recollida de datos como a disculpa fundamental para cambiar o marco legal do uso das linguas no ensino non universitario. Trátase da polémica 'Consulta ás familias' realizada en xuño do 2009, que no seu día foi moi cuestionada polo seu alto custo, 296.000 €. Calquera que teña un mímimo de idea dos fundamentos da estatística sabe que unha mostra de gran tamaño non ten por que ofrecer mellores resultados que outras con menos elementos. O que sí é fundamental é a boa escolla da mostra. Isto asegúrase con técnicas de mostraxe científicas. O proceso seguido neste caso, e sentenciado polo decreto 79/2010, é un exemplo perfecto do que non se debe facer.
Se realmeante se quixera saber cal era o estado de opinión sobre a linguas a empregar no ensino, bastaría con facer unha enquisa a unha mostra verdadeiramente representativa. Pola contra, Anxo Lorenzo quixo xogar a facer estatísticas e argallou unha monstruosidade científica. Vexamos.
A cuestión era obter información sobre as familias dos estudantes no ensino non universitario. Pouco hai que reflexionar sobre a poboación a estudar para concluir que é imposible unha recollida de datos con garantías. No canto de enviar un cuestionario a cada elemento da poboación, ou de escoller unha mostra representativa, tal e como se fai habitualmente nos estudos estatísticos:
Indiana librouse. Pola contra Galicia pode ser posta en ridículo por incluir nas letras dun DOG unha aberración estatística. No funesto decreto 79/2010, o do plurilingüismo sentenciase un kafkiano procedemento de recollida de datos como a disculpa fundamental para cambiar o marco legal do uso das linguas no ensino non universitario. Trátase da polémica 'Consulta ás familias' realizada en xuño do 2009, que no seu día foi moi cuestionada polo seu alto custo, 296.000 €. Calquera que teña un mímimo de idea dos fundamentos da estatística sabe que unha mostra de gran tamaño non ten por que ofrecer mellores resultados que outras con menos elementos. O que sí é fundamental é a boa escolla da mostra. Isto asegúrase con técnicas de mostraxe científicas. O proceso seguido neste caso, e sentenciado polo decreto 79/2010, é un exemplo perfecto do que non se debe facer.
Se realmeante se quixera saber cal era o estado de opinión sobre a linguas a empregar no ensino, bastaría con facer unha enquisa a unha mostra verdadeiramente representativa. Pola contra, Anxo Lorenzo quixo xogar a facer estatísticas e argallou unha monstruosidade científica. Vexamos.
A cuestión era obter información sobre as familias dos estudantes no ensino non universitario. Pouco hai que reflexionar sobre a poboación a estudar para concluir que é imposible unha recollida de datos con garantías. No canto de enviar un cuestionario a cada elemento da poboación, ou de escoller unha mostra representativa, tal e como se fai habitualmente nos estudos estatísticos:1. Douselle aos alumnos (de entre 3 e 18 anos) o cuestionario o que imposibilitou de facto a verificación da chegada do cuestionario a quen realmente ía dirixido. A devolución do cuestionario cuberto pecou do mesmo defecto. Isto invalidaría os resultados en calquera consulta seria.
2. Ao haber pais con varios fillos, de certo que moitos deles cubriron varios cuestionarios, tantos como fillos tiñan. Isto invalidaría os resultados en calquera consulta seria.
3. Tampouco houbo control sobre o destinatario do cuestionario. Non se habilitou forma de detectar se quen cubría o cuestionario era o pai, a nai, un familiar, o propio alumno, ... ou calquera outro que tivera acceso ao mesmo. Isto invalidaría os resultados en calquera consulta seria.
4. O proceso de recollida de datos xenerou unha gran expectación social. Isto fixo que os grupos políticos e os medios de comunicación dirixiran as respostas. Isto invalidaría os resultados en calquera consulta seria.
5. Nos cuestionarios aparecían catro preguntas con resposta pechada, pero tamén había unha quinta na que se pedía: "Comentario ou suxestión que se queira facer". A resposta neste caso non é computable. A ninguén nun estudo serio cometería un erro como este. Isto constata a ignorancia dos creadores do cuestionario.
6. As preguntas deben ser redactadas de forma concreta e precisa. Porén no cuestionario fálase da preferencia da lingua para os libros de texto/ as probas orais e escritas, sen concretar en cales. Tamén se pregunta sobre se o pai gostaría de impartírense aulas en inglés, non se concreta de que materias, nin do peso sobre o total. Cal é a intención das preguntas? Que información obtemos dela? Só podemos extraer informacións xerais sobre a opinión dos pais, eventualmente sobre os seus prexuízos.
7. As preguntas deben ser redactadas de forma clara e inequívoca. Nunha das preguntas fálase de materias 'troncais' cando tal denominación non existe en toda a lexilación vixente e polo tanto é completamente descoñecida para os que deben contestar.
8. Ao ser un documento emitido pola Xunta, de vir redactado en galego, sería neutro, tal e como correspondería a un cuestionario destas características. O cuestionario está escrito todo el en galego e castelán ata extremos paroxísticos. Tendo en conta que o cuestionario trata precisamente do uso das linguas, e que o documento procede precisamente da Consellería de Educación, está mandándose a mensaxe de que a propia Consellería aposta por desprenderse da defensa do galego. Esta falta de coidado
invalidaría os resultados en calquera consulta seria.
En definitiva, estamos diante dun claro caso de escolla dunha mostra non representativa. Os resultados obtidos serán necesariamente nesgados, isto é, os datos non reflicten as verdadeiras características a estudar da poboación. Ademáis os factores para que isto sexa así son múltiples, o que nos dá idea de que o estudo non responde a motivos responsables de coñecemento social senón máis ben a unha estratexia propagandística.
Unha trapallada como a acometida co asunto da consulta pola Consellería de Educación debería ser motivo suficiente de dimisión para os seus responsables. Que ademais se faga desta aberración estatística o fundamento dun decreto legal, é razón para a vergoña de todo un pobo. E que agora se insista en reivindicar con orgullo este atentado contra os fundamentos da ciencia estatística (alén do desprezo pola lingua de noso), vén sendo algo así como anunciar en pleno século XXI que por fin se achou a cuadratura do círculo.
martes, 22 de maio de 2012
Explícoche matemáticas 2.0
Non podo facer outra cousa que darlle os parabéns á iniciativa Explícoche Matemáticas 2.0, un concurso dirixido a todo o alumnado da Facultade de Matemáticas da USC que ten por obxectivo promover a utilización do galego como medio de transmisión das Matemáticas, así como a creatividade do alumnado, a través da realización de curtametraxes de 2 minutos de duración nas que se explique en galego un concepto matemático. O xurado do concurso decidou darlle o premio ao vídeo Factorización en números primos do moañés Juan José Conde Veiga, debido á súa orixinalidade, a súa calidade técnica e ao logro de explicar os conceptos de número primo e factor primo ao grande público.
O vídeo trata de dous amigos que manteñen unha conversa por Skype. Ela estuda matemáticas; el é xordo, e os dous falan nunha mistura de lingua de signos, lingua falada e mensaxes de texto. El viu hai pouco a película “The Cube" por recomendación dela, e non entende a parte que ten que ver cos números primos, e pídelle a ela que llo explique.
O xurado tamén destacou o vídeo A característica de Euler-Poincaré pola súa calidade técnica, un traballo de animación cunha execución impecable. A característica de Euler-Poincaré permite identificar aquelas superficies compactas sempre e cando permitamos unha deformación continua das mesmas (por exemplo, tal e como vemos no vídeo, podemos transformar un cubo nunha esfera; pero nunca poderemos transformar a esfera nunha rosquilla pois para facelo teriamos que furala, e isto atentaría contra a premisa de continuidade). Así, dúas superficies compactas coa mesma característica de Euler-Poincaré, poderán transformarse unha noutra con continuidade.
O xurado tamén destacou o vídeo A característica de Euler-Poincaré pola súa calidade técnica, un traballo de animación cunha execución impecable. A característica de Euler-Poincaré permite identificar aquelas superficies compactas sempre e cando permitamos unha deformación continua das mesmas (por exemplo, tal e como vemos no vídeo, podemos transformar un cubo nunha esfera; pero nunca poderemos transformar a esfera nunha rosquilla pois para facelo teriamos que furala, e isto atentaría contra a premisa de continuidade). Así, dúas superficies compactas coa mesma característica de Euler-Poincaré, poderán transformarse unha noutra con continuidade.
domingo, 20 de maio de 2012
Ramón María Aller Ulloa
Vídeo da USC sobre a inmensa e modesta figura de Don Ramón María Aller Ulloa, o astrónomo de Lalín. Con guión de Docobo, director do observatorio universitario.
De José ángel Docobo tamén é esta pequena reseña biográfica, así como o artigo Ramón María Aller Ulloa, precursor da investigación astronómica en Galicia, publicado no volume XXX da Real Academia Gallega de Ciencias.
Outro documento de fácil acceso o traballo de Vidal Abascal sobre Aller, pois fora editado con motivo das IX JAEM (Jornadas para el Aprendizaje y la Enseñanza Matemática) celebradas en Lugo no ano 1999.
Probablemente a obra máis coñecida de Aller sexa o libro de divulgación publicado pola USC, 'Astronomía a simple vista' . A respecto deste libro eu nunca deixo de lembrar que o 20 de maio do 1936, pouco antes do golpe de estado, dábase conta da noticia da intención de Ramón María Aller de publicar o que probablemente sería a idea orixinal deste libro, tratábase de 'Astronomía a ollo ceibe', o primeiro libro de divulgación científica en galego, un libro do que nunca máis se soubo nada.
domingo, 6 de maio de 2012
Hipercubo de 4 dimensións
Un cubo de dimensión 0 é un punto, un de dimensión 1 será un segmento. Os cubos de dimensión 2 son os cadrados e os de dimensión 3 son, precisamente, os cubos. Pero como son os cubos de 4 dimensións?
Un segmento ten 2 vértices.
Un cadrado ten 4 vértices e 4 arestas.
Un cubo ten 8 vértices, 12 arestas e 6 caras.
Un hipercubo terá... É un moi bo exercicio mental intentar razoar coherentemente o número de elementos xeométricos que identifican un hipercubo de 4 dimensións. Despois de pensalo un pouco, podemos ver unha reflexión sobre o tema que fai João Nuno Tavares nesta aplicación da Universidade do Porto.
Para continuar remexendo no tema, vai este vídeo con toda unha serie de perspectivas desde as que observar o hipercubo.
Un segmento ten 2 vértices.
Un cadrado ten 4 vértices e 4 arestas.
Un cubo ten 8 vértices, 12 arestas e 6 caras.
Un hipercubo terá... É un moi bo exercicio mental intentar razoar coherentemente o número de elementos xeométricos que identifican un hipercubo de 4 dimensións. Despois de pensalo un pouco, podemos ver unha reflexión sobre o tema que fai João Nuno Tavares nesta aplicación da Universidade do Porto.
Para continuar remexendo no tema, vai este vídeo con toda unha serie de perspectivas desde as que observar o hipercubo.
xoves, 3 de maio de 2012
Unha foto de 4 millóns de decimais de π
Shigeru Kondo e Alexander Yee son os xaponeses que obtiveron o pasado ano 10 billóns de cifras decimais do número π. Segundo informan no seu web deberon empregar máis dun ano de cálculos: do 10 de outubro do 2010 ao 16 do mesmo mes do 2011. Polo medio do cálculo sucedeu o desastre do tsunami que destrozou a zona de Fukushima pero que non afectou ao proceso.
Pero desta volta o que quixera é aproveitar a noticia para recomendar un web, ou se preferides, unha foto que contén os 4 primeiros millóns de díxitos do número π. Cada díxito é substituído por un píxel segundo o seguinte código:
Ademais este recurso permítenos facer unha búsqueda dunha sucesión de varios díxitos consecutivos entre os decimais de π. Por exemplo, se introducirmos catro ceros: '0000' obtemos como resposta que a súa primeira aparición obterémola a partir do lugar decimal número 13.390. Ademais as cifras anteriores a esta restra de catro ceros son 585293095 e as posteriores son 907151.
Pero desta volta o que quixera é aproveitar a noticia para recomendar un web, ou se preferides, unha foto que contén os 4 primeiros millóns de díxitos do número π. Cada díxito é substituído por un píxel segundo o seguinte código:
Ademais este recurso permítenos facer unha búsqueda dunha sucesión de varios díxitos consecutivos entre os decimais de π. Por exemplo, se introducirmos catro ceros: '0000' obtemos como resposta que a súa primeira aparición obterémola a partir do lugar decimal número 13.390. Ademais as cifras anteriores a esta restra de catro ceros son 585293095 e as posteriores son 907151.
Por certo, a cifra decimal situada no 10 billonésimo lugar é un....x
sábado, 28 de abril de 2012
Album da ciencia: os matemáticos galegos
O Consello da Cultura Galega (CCG) tráenos á arañeira da rede un novo recurso que creo moi recomendable para o ensino e divulgación da ciencia. Trátase do Album da Ciencia, unha especie de dicionario on-line de biografías de científicos galegos. Polo momento temos un gorentoso adianto do que vai ser unha colección de 300 entradas cunha calidade excepcional, posiblemente debida aos coñecementos dunha considerable nómina de especialistas que podemos consultar aquí.
Polo de agora contamos cunha pequena mostra de biografías. Como por afición e traballo o que máis me interesa é o apartado dos matemáticos, recollo o publicado ata o momento polo CCG
Os matemáticos galegos
José Antonio López y Nobal (1763-1824). Exerceu como profesor de matemáticas na Academia de Guardas Marinas de Ferrol e estivo destinado no seu Observatorio Astronómico, o primeiro dunha institución en Galicia. É o autor dunha obra enciclopédica, Consideraciones Generales, na que se fai evidente a súa formación matemática.
Ángel Laborde Navarro (1773-1834). Foi o primeiro profesor de matemáticas do Real Colegio Militar de Santiago. Edita un libro de matemáticas básicas para o seu uso docente, probablemente o primeiro libro destas características imprimido en Galicia.
Pedro Antonio Cerviño Núñez (1757-1816). Natural de Campolameiro, destaca o seu labor como director da Escola de Náutica de Buenos Aires, onde impulsou un plan de estudos centrado nas matemáticas, sendo precursor desta ciencia na Arxentina.
Juan Jacobo Durán Loriga (1854-1911). Membro fundador da RSME, publicou unha gran cantidade de artigos de matemáticas. Destacan as súas investigacións nunha rama das matemáticas moi de moda a finais do XIX, a xeometría do triángulo.
Ramón María Aller Ulloa (1878-1966). Coñécese por ser o precursor do estudo da astronomía en Galicia. Foi profesor de Xeometría analítica e Análise Matemática na universidade compostelana. Como dato curioso e significativo querría destacar que no ano 1936 anunciase o que posiblemente podería ser o primeiro libro de divulgación científica en galego: Astronomía a ollo ceibe. A guerra civil e a dictadura impediron que isto fose posible.
Ademais deste Album da Ciencia, o Consello da Cultura Galega xa tiña outra colección ben interesante do mesmo estilo, o Album de Mulleres. Del destacaría o apartado dedicado a María Josefa Wonenburger Planells. Unha figura mundial das matemáticas [web]. Contén gran cantidade de recursos.O 28 de novembro do 2010 celebrouse nas dependencias do Consello da Cultura Galega a xornada María Josefa Wonenburger Planells na creación de coñecemento [web]. Inclúense audios coas intervencións da xornada.
Otra muller deste Album, tamén figura destaca nas matemáticas e astronomía (traballou con Aller Ulloa), foi Antonia Ferrín Moreiras (1914-2009), coñecida como a contadora de estrelas.
luns, 23 de abril de 2012
'D': o terror e o axioma de Pasch
"D" - animated short film from Closed Eye Visuals on Vimeo.
Nesta excepcional curta, orlada con varios premios, relátase unha historia de terror sobre un libro de matemáticas.
Nos primeiros momentos da animación podemos ver escrito na páxina sobre a que se desenvolve a acción o axioma de Pasch, que é un deses axiomas da xeometría plana que sen enuncialos explícitamente, Euclides tivo que usar nos seus Elementos. Hai máis casos, en ningún lugar dos Elementos se indica se é posible que se corten entre si dúas rectas, dúas circunferencias, rectas con circunferencias,...
O axioma dinos que se unha recta corta un lado dun triángulo e non pasa por ningún dos seus vértices, debe cortar outro dos lados.
Moritz Pasch, matemático de finais do XIX, tivo unha importante influencia en Hilbert na súa concepción da xeometría. Lembremos que Hilber dicía que tanto lle tiña falar de puntos, rectas e segmentos como de cadeiras, mesas e xarras de cervexa. O significado desta declaración reside en que non debemos supoñer dos conceptos máis cousas que as que se tiran exclusivamente dos axiomas.
O axioma de Pasch é un dos axiomas de ordenación dos Fundamentos da Xeometría de Hilbert
Vía ZTFNews.org
Nesta excepcional curta, orlada con varios premios, relátase unha historia de terror sobre un libro de matemáticas.
Nos primeiros momentos da animación podemos ver escrito na páxina sobre a que se desenvolve a acción o axioma de Pasch, que é un deses axiomas da xeometría plana que sen enuncialos explícitamente, Euclides tivo que usar nos seus Elementos. Hai máis casos, en ningún lugar dos Elementos se indica se é posible que se corten entre si dúas rectas, dúas circunferencias, rectas con circunferencias,...
O axioma dinos que se unha recta corta un lado dun triángulo e non pasa por ningún dos seus vértices, debe cortar outro dos lados.
Moritz Pasch, matemático de finais do XIX, tivo unha importante influencia en Hilbert na súa concepción da xeometría. Lembremos que Hilber dicía que tanto lle tiña falar de puntos, rectas e segmentos como de cadeiras, mesas e xarras de cervexa. O significado desta declaración reside en que non debemos supoñer dos conceptos máis cousas que as que se tiran exclusivamente dos axiomas.
O axioma de Pasch é un dos axiomas de ordenación dos Fundamentos da Xeometría de Hilbert
Vía ZTFNews.org
mércores, 14 de marzo de 2012
Xeometría en galego: a páxina de Paulo Porta
Andaba pola arañeira da rede buscando recursos de matemáticas que me poideran ser de utilidade e fun dar cunha impresionante perla.
Menos mal que existe unha plataforma catalá, Creamat, que si mantén unha ligazón aos contidos aos que me estou a referir: a páxina de Paulo Porta, xa que estrañamente (?), este portal non está ligado desde o proxecto Abalar, a pesar de que algúns recursos do web foron premiados pola Xunta dentro do programa SIEGA (Sistema de Información da Educación Galega). Un dos apartados, que levou un premio SIEGA no 2003 trata sobre tanxencias. O outro traballo premiado é un impresionante percorrido polos poliedros e as súas propiedades. Ademais dunha presentación dos poliedros regulares, semiregulares e estrelas, o web ofrécenos arquivos pdf co desenvolvemento plano dunha enorme colección de poliedros e un apartado sobre a teselación do espazo.
Isto non é todo. No web de Paulo Porta tamén temos acceso a 18 demostracións visuais do teorema de Pitágoras.
E aínda hai máis. Case 30 métodos xeométricos para obter a cuadratura do cículo. Trátase, como se pode supoñer, de métodos que aproximan a área do círculo. Entre outras marabillas podemos ver un par de cuadraturas do padre Sarmiento, unha delas cunha aproximación excepcional, que nos daría un valor para =3,1415926628 (as súas primeiras cifras son
=3,1415926628 (as súas primeiras cifras son  =3,141592653589). O método de Sarmiento ofrécenos un método para a obtención da área do cículo equivalente unha precisión de
=3,141592653589). O método de Sarmiento ofrécenos un método para a obtención da área do cículo equivalente unha precisión de  con 7 cifras decimais correctas!
Ademais de todo isto a páxina contén outros recursos relacionados co debuxo ou coa obra artística do autor.
con 7 cifras decimais correctas!
Ademais de todo isto a páxina contén outros recursos relacionados co debuxo ou coa obra artística do autor.
Isto non é todo. No web de Paulo Porta tamén temos acceso a 18 demostracións visuais do teorema de Pitágoras.
E aínda hai máis. Case 30 métodos xeométricos para obter a cuadratura do cículo. Trátase, como se pode supoñer, de métodos que aproximan a área do círculo. Entre outras marabillas podemos ver un par de cuadraturas do padre Sarmiento, unha delas cunha aproximación excepcional, que nos daría un valor para
Subscribirse a:
Publicacións (Atom)