Teorema de Hall: o teorema dos matrimonios

 Na entrada anterior presentaramos o seguinte resultado

Teorema do matrimonio de Hall. Dado un grafo bipartito $G=(X,Y)$, unha condición necesaria e suficiente para que $X$ teña un emparellamento perfecto (condición de Hall) é que  $\forall A\subset X$ se verifique que $ \left| A \right|\le \left| N\left( A \right) \right|$

Segundo a Wikipedia o teorema de Hall recibe o nome de teorema do matrimonio debido a un artigo do ano 1950 no que Halmos e Vaugan se refiren ao teorema para tratar a seguinte cuestión:

"Supoñamos que un grupo de mozos [...] coñece un conxunto finito de mozas. Baixo que condicións é posible que cada un deles se case cunha das súas coñecidas?"

Desde un punto de vista da sociedade actual o enunciado do problema fica algo desfasado. Con todo, o problema pode levarnos a unha ampliación do noso punto de vista matemático. Para iso seguiremos o libro de Gilbert Strang, Introduction to applied mathematics (Wellesley-Cambidge Press 1986).

Dadas $n$ señoritas , que por seren de xénero feminino identificaremos por $f_{1}, f_{2},..., f_{n}$ e outros tantos cabaleiros $c_{1}, c_{2},..., c_{n}$ estableceremos unha matriz $A=\left( a_{ij} \right)$ onde $a_{ij}=1$ se $f_{i}$ e $c_{j}$ están dispostos a casar. No caso contrario escribiremos $a_{ij}=0$. Se for posible establecer $n$ matrimonios significa que hai un emparellamento perfecto no grafo asociado. Vexamos un exemplo no que puidemos establecer $4$ matrimonios que son os que aparecen marcados nun recadro.

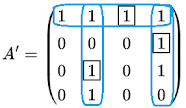
Porén no seguinte caso non é posible celebrar máis que tres bodas: $\left( f_{1},c_{3} \right), \left( f_{2},c_{4} \right)$ e $\left( f_{3},c_{2} \right)$:

Esta matriz dá lugar ao seguinte grafo no que resaltamos con arestas grosas os tres matrimonios:

Se escollo as tres últimas filas $\left\{ f_{2},f_{3},f_{4} \right\}$ comprobo inmediatamente que a súa veciñanza está formada por só dúas columnas $\left\{ c_{2},c_{4} \right\}$. Isto significa que non se verifica a condición de Hall. De aí que non poidan establecerse $4$ matrimonios.

Voulle chamar liña a unha fila ou columna. Comprobarás que marcando as tres liñas rodeadas en azul teño cubertos todos os $1s$ da matriz $A'$. Isto vén a conto do seguinte teorema que é equivalente ao de Hall:

Terorema de Köning-Egerváry. Nunha matriz de $0s$ e $1s$ o máxino número de matrimonios é igual ao mínimo número de liñas que cubren todos os $1s$

Todo isto podémolo relacionar con outras cousas coñecidas. Consideremos a matriz $A$ como un taboleiro de xadrez de dimensións $n\times n$ onde cada elemento é un escaque. Propoñemos o reto de colocar o maior número posible de torres sen que se ameacen entre sí coa restrición de que só está permitido colocalas nos escaques marcados con $1$. Evidentemente o xogo é esencialmente o mesmo problema que o do matrimonio.

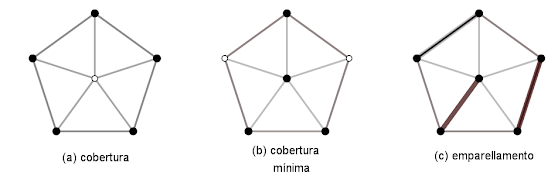
Imos dar algo máis de terminoloxía para ampliar a perspectiva deste resultado. Unha cobertura $K$ dun grafo é un conxunto de vértices do grafo tal que todas as arestas do grafo teñen polo menos un vértice en $K$. Sempre será interesante obter unha cobertura mínima, isto é, aquela que teña o menor número de vértices posible. A seguinte figura pode aclararnos a situación. Nela están marcados en negro os vértices que forman a cobertura.

Os emparellamentos podemos consideralos como coberturas. Ademais dado calquera emparellamento $M$ e calquera cobertura $K$, verificarase claramente que $\left| M \right|\lt \left| K \right|$. Con estes vimbios podemos reescribir o

Teorema de Köning-Egerváry. Nun grafo bipartito o número de arestas dun emparellamento máximo é igual ao número de vértices dunha cobertura mínima.

Tamén podemos afrontar o problema desde un punto de vista alxébrico. Volvendo ás matrices, do que se trata é de obter o seu rango. Se hai unha fémina á que non lle guste ningún cabaleiro teremos unha fila só con $0s$. Neste caso xa sabemos que o determinante da matriz será nulo. Como todos os valores son $1s$ e $0s$ o teorema de Hall establece que para que poidan celebrarse $n$ matrimonios, ou o que é o mesmo, que a matriz dos matrimonios sexa regular,  vai ter que verificarse calquera das tres seguintes condicións equivalentes

• Non existe unha submatriz de $0s$ de dimensión $r\times s$ con $r+s\gt n$
• A cada subconxunto de $1 \le r\le n$ mozas lles gustan polo menos $r$ mozos
• A cada subconxunto de $1 \le s\le n$ mozos lles gustan polo  menos $s$ mozas

Na seguinte entrada veremos máis aplicación do teorema de Hall.