por Andrés Ventas
Fraccións continuas teito
Unha fracción continua teito ($fct$) é unha fracción continua na que usamos a función teito para obter os seus coeficientes. Os seus converxentes $\frac{p_i}{q_i}$ obtéñense mediante unha recorrencia de resta,
$p_{-1}=1, \ p_{0}=c_0, \ p_i=c_i p_{i-1} - p_{i-2}$.
$q_{-1}=0, \ q_{0}=1, \ q_i=c_i q_{i-1} - q_{i-2}$.
Para o cálculo da fracción continua, se $x$ é racional usamos o algoritmo de Euclides coa función teito e se o número e irracional usamos unha iteración sobre o inverso de $x$ restando en cada paso o valor teito do resultado.
Hai varias notacións.É moi cómoda a reducida, choendo os coeficientes entre símbolos da función teito $\lceil c_0, c_1, c_2, c_3, \cdots \rceil$.
A notación tradicional é \[ \mathrm{x}= c_0-\cfrac{1}{c_1-\cfrac{1}{c_2-\cfrac{1}{c_3- \cdots\vphantom{\cfrac{1}{1}} }}} \]
E a maiores hai outra notación semireducida $c_0 - \dfrac{1}{c_1 \ -} \ \dfrac{1}{c_2 \ - } \ \dfrac{1}{c_3 \ - } \ \dfrac{}{\ldots} $,
Vexamos dous exemplos de cálculo:
Con Euclides teito, calculamos a $fct$ de $\dfrac{93}{20}$ e os seus converxentes,
|
|
Así $\dfrac{93}{20}=\lceil 5, 3, 7 \rceil = 5-\cfrac{1}{3-\cfrac{1}{7\vphantom{\cfrac{1}{1}} }}$. (Como fracción continua regular $\dfrac{93}{20}=[4, 1, 1, 1, 6 ]).$
Agora con inverso iterativo, calculamos $\sqrt{3} \approx 1.7320$ e os seus converxentes,
|
|
Así temos $\sqrt{3}=\lceil 2, 4, 4, \cdots \rceil$,
sendo $\sqrt{3} \approx 1.7320$ e o cuarto converxente $\dfrac{97}{56} \approx 1.7321$.
Comparten moitas propiedades coas fraccións continuas regulares, mais evidentemente teñen as súas pecularidades. No libro de Sergey Khrushchev, Orthogonal Polynomials and Continued Fractions temos un minucioso tratado.
As $fct$ converxen sempre polo lado superior.
Nalgúns casos as $fct$ dan o menor número de pasos, aínda que normalmente son peores en número de pasos. De feito non cumpren coa constante de Khinchin, porque se atoan nos coeficientes, fundamentalmente no $2$.
No 1657 Brouncker atopa, seguindo outro camiño, unha fracción continua teito para solucionar a ecuación de Pell $x^2 - 2y^2 =1$, onde as solucións son certos converxentes da $fct=\lceil 6, 6, 6, \ldots \rceil$, con recorrencia $x_n=6x_{n-1}-x_{n-2}$ e por tanto a solución consiste en resolver a ecuación $x=6-\dfrac{1}{x}$, que dá $x=3+2\sqrt{2}$. (Lema 2.21 do libro de Khrushchev).
Se se permiten coeficientes en $\mathbb{Q}$ ou mesmo en $\mathbb{C}$ os resultados son máis interesantes aínda, serían funcións teito xeneralizadas que van en paralelo coas fraccións continuas xeneralizadas.
Fraccións continuas mixtas
Na fracción continua mixta ($fcm$) usamos a función teito ou chan en cada paso en función do menor residuo. A notación sería igual que a da fracción continua regular mais levando un superindice "$\mathbf{-}$" sobre os coefcientes que se obteñan coa función teito $[ c_0, c_1^{\mathbf{-}}, c_2^{\mathbf{-}}, c_3, \cdots ]$.
Para obter os seus converxentes $\dfrac{p_i}{q_i}$ temos recorrencia de suma ou resta en función do superíndice do coeficiente $c_{i-1}$, restamos cando $c_{i-1}^{\mathbf{-}}$ ten superíndice negativo.
$p_{-1}=1, p_{0}=c_0, p_i=c_i p_{i-1} \pm p_{i-2}$.
$q_{-1}=0, q_{0}=1, q_i=c_i q_{i-1} \pm q_{i-2}$.
(Signo negativo se $c_{i-1}$ ten superíndice $\mathbf{-}$).
Este tipo de fracción dá o menor número de pasos no algoritmo de Euclides e igualmente dá o menor número de termos na fracción continua. Outra vez vexamos dous exemplos.
Con Euclides mixto, calculamos a $fcm$ de $\frac{2114}{61}$, e os seus converxentes,
|
|
Por tanto $\dfrac{2114}{61}=[ 35^{\mathbf{-}}, 3^{\mathbf{-}}, 10, 2]$.
Xa temos unha moi boa cousa positiva das $fcm$ pois obtemos o $mcd$ nun menor número de pasos e por tanto tamén o multiplicativo modular inverso.
Constantes das montañas de Galicia
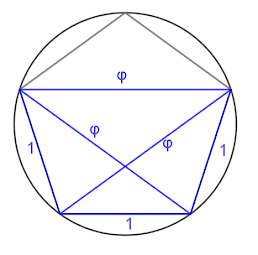
Chámanse medias ou constantes metálicas os valores das fraccións continuas que teñen todos os seus coeficientes iguais, a máis famosa precisamente a proporción aurea $\varphi=\frac{1+\sqrt{5}}{2}=1.618033\ldots$ con fracción continua regular $[1,1,1,1, \ldots]$.
Así que imos aproveitar para definir, usando as $fct$ de forma similar, as constantes das montañas de Galicia. Temos que $fct=\lceil 3, 3, 3, \ldots \rceil = \frac{3+\sqrt{5}}{2}=2.618033\ldots$ que como vemos é $\varphi + 1$ e a esta constante ímoslle chamar Pena Trevinca pois o nome évos ben acaído para ese conxunto de treses.
É fácil demostrar que o valor para calquera $fct$ cos coeficientes repetidos é $$\lceil c, c, c, c, \ldots \rceil=\dfrac{c+\sqrt{c^2-4}}{2}$$ por tanto podemos asignar unha constante a cadanseu monte:
O caso da $fct=\lceil 2, 2, 2, \ldots \rceil$ é particular pois ten como solución unha constante enteira $1$, así que imos deixar esa constante para o Monte da Guía en Vigo que ten só $100$ metros.
| $fct$ | Constante | Monte | Altura |
|---|---|---|---|
| $ \lceil 2, 2, 2, \ldots \rceil$ | $\frac{2+\sqrt{0}}{2}=1$ | Monte da Guía (Vigo) | 100 metros |
| $ \lceil 3, 3, 3, \ldots \rceil$ | $\frac{3+\sqrt{5}}{2}=2.618033$ | Pena Trevinca (Serra do Eixo) | 2127 metros |
| $ \lceil 4, 4, 4, \ldots \rceil$ | $\frac{4+\sqrt{12}}{2}=2+\sqrt{3}=3.732050$ | Cuíña (Serra dos Ancares) | 1987 metros |
| $ \lceil 5, 5, 5, \ldots \rceil$ | $\frac{5+\sqrt{21}}{2}=4.791287$ | Manzaneda (Serra da Queixa) | 1781 metros |
| $ \lceil 6, 6, 6, \ldots \rceil$ (Brouncker) | $\frac{6+\sqrt{32}}{2}=3+2\sqrt{2}=5.828427$ | Formigueiros (Serra do Courel) | 1639 metros |
| $ \lceil 7, 7, 7, \ldots \rceil$ | $\frac{7+\sqrt{45}}{2}=6.854101$ | O Turrieiro (Serra da Enciña da Lastra) | 1612 metros |
| $ \lceil 8, 8, 8, \ldots \rceil$ | $\frac{8+\sqrt{60}}{2}=4+\sqrt{15}=7.872983$ | Monte Faro (Serra do Faro) | 1187 metros |
| $ \lceil 9, 9, 9, \ldots \rceil$ | $\frac{9+\sqrt{77}}{2}=8.887482$ | O Cadramón (Serra do Xistral) | 1056 metros |