Algún día tería que relatar as miñas desventuras no CAP (Curso de Adaptación Pedagóxiga), un curso que xogaba aproximadamente o mesmo papel que o Máster de Profesorado actual. Só comentarei que, cando me faltaba só unha sesión para rematalo, abandoneino, farto. Efectivamente, estaba farto de ver como quen presumiblemente tiña que dar directrices sobre orientacións didácticas actuaba como un terrorista pedagóxico. Recordo unha materia levada por dous profesores, un home gordo e unha muller fraca. Impartían clase xuntos. Pasaban todo o tempo discutindo. Iso podería estar ben se fose algo pensado e preparado. Non era o caso. Nunha ocasión pasaran toda a sesión dándolle voltas a como tratar aos rapaces zurdos. Se conviña, ou non, forzalos a escribir coa man dereita. Non era esta un tema que houbese que tratar no CAP, só foi unha ocorrencia máis desa parella infame de profesores. Desde aquela quedoume a impresión que unha clase levada en parella tiña que ser necesariamente un fracaso. Non é así. Isto demostráronolo Nicanor Alonso e Miguel Mirás o pasado venres 16/05/2025 na charla que viñeron impartir ao IES Antón Losada Diéguez ao alumnado de 1º de Bacharelato. O segredo do éxito dunha clase en tándem? O mesmo que o dunha clase impartida por unha persoa soa: traballo e preparación.
Algún día tería que relatar as miñas desventuras no CAP (Curso de Adaptación Pedagóxiga), un curso que xogaba aproximadamente o mesmo papel que o Máster de Profesorado actual. Só comentarei que, cando me faltaba só unha sesión para rematalo, abandoneino, farto. Efectivamente, estaba farto de ver como quen presumiblemente tiña que dar directrices sobre orientacións didácticas actuaba como un terrorista pedagóxico. Recordo unha materia levada por dous profesores, un home gordo e unha muller fraca. Impartían clase xuntos. Pasaban todo o tempo discutindo. Iso podería estar ben se fose algo pensado e preparado. Non era o caso. Nunha ocasión pasaran toda a sesión dándolle voltas a como tratar aos rapaces zurdos. Se conviña, ou non, forzalos a escribir coa man dereita. Non era esta un tema que houbese que tratar no CAP, só foi unha ocorrencia máis desa parella infame de profesores. Desde aquela quedoume a impresión que unha clase levada en parella tiña que ser necesariamente un fracaso. Non é así. Isto demostráronolo Nicanor Alonso e Miguel Mirás o pasado venres 16/05/2025 na charla que viñeron impartir ao IES Antón Losada Diéguez ao alumnado de 1º de Bacharelato. O segredo do éxito dunha clase en tándem? O mesmo que o dunha clase impartida por unha persoa soa: traballo e preparación.
Examinaron moitos máis tópicos e sempre dunha forma clara e coordinada. Claro que, no canto de ser explicados en parella, tal e como o fixeron eles, case todos podían ter sido tratados por un só conferenciante. Comento isto porque un dos capítulos necesitaba de dúas persoas para poder desenvolvelo. A min foi o que máis me sorprendeu e agradou. Trátase do truco das 5 cartas de Cheney, asunto do que, por certo, xa se ocupara no seu día Jota nesta entrada, O mellor truco de cartas. O enunciado promete. Vexamos como se desenvolveu.
As cinco cartas de Cheney
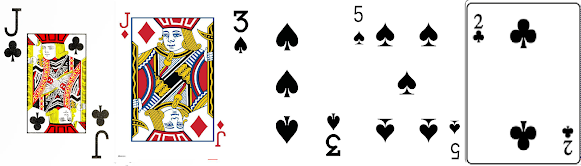
Un dos dous conferenciantes marchou da sala; chamémoslle mago. O outro, chamémoslle axudante, pediu a un voluntario que escollera cinco cartas dunha baralla francesa completa (52 cartas, 13 de cada un dos paus, a saber: corazóns ♡ , diamantes ♢, picas ♠ e trevos ♣). Entón o axudante colocou catro desas cartas sobre unha mesa e deixou a quinta ao final, virada cara abaixo.

Cando volveu o mago e veu esas cartas sobre a mesa, concentrouse un momento e adiviñou cal era a carta que estaba boca abaixo.
Estaba claro que elaboraran un código para identificar as cartas pois diso trataba a conferencia. Pero teñamos presente que non poden saber previamente cales son as cartas que se van escoller polo que o código debería estar montado sobre a ordenación das cartas. Está claro que podemos establecer unha orde entre todas elas. En primeiro lugar, os números (do 1 ao 13) axudan moito. E que pasa se dúas cartas teñen o mesmo valor numérico? Daquela basta con que o mago e o seu axudante establezan unha orde dos paus. Podería ser, por exemplo, a orde do abecedario pola primeira letra: corazóns ♡ < diamantes ♢< picas ♠ < trevos ♣. Con todo, hai un problema, as $4$ cartas que quedan visibles só poden ordenarse de $4!=24$ formas distintas.
Para salvar esta dificultade hai que aproveitar todas as vantaxes que nos dá o desenvolvemento do truco. Teñamos presente que é o axudante quen escolle a carta que se coloca boca abaixo. Polo principio do pombal, dadas $5$ cartas, é seguro que vai haber polo menos dúas do mesmo pau. Isto permite que o axudante escolla dúas cartas do mesmo pau e coloque unha cara abaixo e a outra pode colocala na primeira posición. No noso exemplo a primeira carta era o rei de trevos, velaí que a carta a adiviñar será tamén un trevo. Agora quédannos outras tres cartas visibles que nos deben permitir identificar o número da carta oculta. Outra vez, se ordenamos esas tres cartas termos un total de só $3!=6$ posibilidades e nós necesitamos 13. Aquí é onde entra en xogo a aritmética modular.
Facemos unha identificación do valor da carta cos números das congruencias de $\mathbb{Z}_{13}$. A diferenza entre dous destes valores nunca é maior que $6$. As cartas que escolleu o axudante eran a $J$ e o $2$ de trevos. A súa diferenza é de $4$ unidades. Ocultando o $2$ só lle ten que dicir ao seu compañeiro que debe sumarlle $4$ unidades á $J$. En aritmética modular $11+4\equiv 2 (mód 13)$. O código utilizado para indicar o número a sumar é o que explicamos de seguido. Vou identificar o $1$ co valor máis baixo das tres cartas, o $2$ co intermedio e o $3$ co maior. Daquela establezo a seguinte relación entre as $6$ ordenacións e o $6$ números que debo sumar (módulo 13) ao valor da primeira carta: