Dúas fendas de luz: o libro de Rózsa Péter e as matemáticas en galego.1

Ao rematar a carreira, para enfrontarme ao que osmaba que sería o meu destino profesional, a docencia, procurei en diversos libros un punto no que agarrarme coa esperanza de que me desen algunha indicación de como asumir o reto baixo unhas directrices minimamente dignas. Non me estou referindo a libros texto, no único que podía achar era "o que", estaba á procura do "como". Daquela a oferta non era moi abondosa, pero percorrín moitos libros de divulgación, outros específicos de educación das matemáticas, dos que trataban da resolución de problemas, moitos sobre a historia e tamén algúns sobre filosofía da ciencia ou sobre a cultura matemática en xeral. Pero buscaba algo que, con todo, non daba atopado. Quizais porque tampouco sabía moito o que estaba a pescudar. Cando estou vendo o final do meu labor docente, por fin achei ese libro: "Xogando co infinito" de Rózsa Péter (1905-1977). Felizmente este texto

foi publicado polo Consello da Cultura Galega (CCG), con tradución do profesor da Facultade de Matemáticias, Felipe Gago.

O pasado xoves 22/06/2023 presentouse a edición deste libro na aula magna da Facultade de Matemáticas. O primeiro que chama a atención é que no acto estivera presente Valentín García, o Secretario Xeral de Política Lingüística, o mesmo que defende o decreto que prohíbe o ensino das matemáticas en galego. Por isto tanto a decana da Facultade de Matemáticas, Elena V. Cendón,  como a presidenta do CCG, Rosario Álvarez, comezaron as súas intervencións cunha frase de Julio Rodríguez, presidente de AGAPEMA: "xa é hora de abrir unha fenda de luz e deixar de prohibir o galego no ensino das matemáticas". Valentín viuse na obriga de responder pero só conseguiu farfallar unha desculpa falsa, nun intento, imposible, de querer quedar ben. 

Elena Vázquez Cendón explicou que o proxecto xurdira cando o premio Abel de 2005,  Peter Lax,  visitou Santiago de Compostela dentro do programa ConCiencia do 2007. Lax foi entrevistado pola periodista Elisa Álvarez quen, ante a idea de que todo matemático tivo alguén que o inspirou, inquiriulle sobre o seu caso. Peter Lax contestou que a súa inspiradora foi unha muller, Rózsa Péter, que escribira o mellor libro popular de matemáticas, "Xogando co infinito". Ao pouco Elena encargoulle o traballo de tradución a Felipe Gago. Hoxe, ademais da publicación física o CCG permite o acceso virtual a esta publicación.  

Na súa intervención, Felipe Gago debullou, cunha fermosa presentación dixital, parte do contido do libro. Vou intentar reproducilo, quizais con algunhas modificacións.

Aprendiz de meiga

Todo comeza nunha aula. Susana, unha alumna que rebordaba curiosidade, Susana, comprobara que efectuar a suma de todos os naturais ata un impar, por exemplo 7, daba o mesmo resultado que multiplicar por 7 o número do medio.

Eva, unha compañeira da clase, deu coa chave do asunto. $4\cdot7$ non é outra cousa que sumar $4$ sete veces. Se comparamos as dúas sumas

Veremos que o primeiro $4$ é $3$ unidades superior a $1$, pero isto compénsase co último $4$, que é $3$ unidades inferior a $7$. Da mesma maneira o segundo $4$ é $2$ unidades máis que $2$, pero isto compénsase con que o penúltimo $4$ sexa $2$ unidades inferior a $6$. Finalmente o terceiro e o antepenúltimo $4$ son respectivamente $1$ unidadade máis e $1$ unidade menos que $3$ e $5$. Velaí que as dúas sumas teñan que dar o mesmo.

Neste punto Rózsa introduce a famosa lenda de como Gauss de neno, conseguira realizar a suma dos 100 primeiros números naturais: $1+2+3+4+....+96+97+98+99+100$. O proceso é esencialmente o mesmo que o que pasamos a describir para a suma dos 4 primeiros números. Coloquemos a suma tamén en orde inversa e despois sumemos o primeiro número co último, o segundo co penúltimo, e así sucesivamente. Así obtemos sempre $5$ como resultado

De aí que o dobre da suma buscada é igual a $5+5+5+5+5=4\cdot5=20$ polo que a suma será a súa metade $1+2+3+4+5=10$. Ademais este proceso, como vemos, non ten por que restrinxirse a sumas ata un número impar, como sucedía antes. Conviña repetir este proceso para outros casos como a suma dos 5 ou dos 7 primeiros números. Incluso podemos ver que podemos aplicalo a unha progresión aritmética calquera.

Neste caso a suma será a metade de $18\cdot5=90$, isto é $5+7+9+11+13=45$

Rózsa Péter non lles dá aos alumnos a fórmula para obter a suma dos termos duna progresión aritmética. Ofrécelle problemas que poden abordar e fainos protagonistas do seu descubrimento, ademais conecta ese achádego co mito gausiano facéndoos partícipes da historia das matemáticas. Isto xa sería suficiente, pero aínda hai máis. O método que vimos de presentar aparece noutros ámbitos das matemáticas. Todos sabemos como medir áreas de rectángulos.

Se tomamos como unidade o cadrado sombreado enseguida vemos que a área deste rectángulo é de $3\cdot8$, basta multiplicar a base pola altura para obtela. Pero enseguida xurde un problema. Se pretendemos obter a área dun triángulo como o seguinte

temos dificultades en completar a área sombreada. A solución vén de aplicar a mesma metodoloxía que a usada para achar as anteriores sumas. No canto dun triángulo, collamos dous, agora formarán un rectángulo

polo que para determinar a área do triángulo bastará con partir pola metade a deste novo rectángulo.

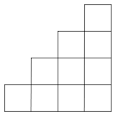
Se continuamos pola senda xeométrica, as anteriores sumas poderían representarse formando unha escaleira

Nesta figura temos representada a suma $1+2+3+4$. Volvamos a aplicar o mesmo procedemento, dupliquemos a figura e rotémola 180º, temos...

... un rectángulo de área $4\cdot5=20$ de aí que a suma buscada sexa, coma antes, 10.

En que circunstancias temos que sumar desde 1 ata un determinado número? Velaquí un problema que responde a esta cuestión

Problema. Determina o número de diagonais dun octógono

Unha boa maneira de abordalo é considerar unicamente os vértices do octógono e comezar a trazar todos os segmentos posibles entre eles. Se conseguimos facelo ao final só teriamos que restarlle os 8 lados do octógono. Comecemos polo vértice $1$, desde el podemos trazar sete segmentos ata os outros sete puntos; se continuamos co vértice $2$ veremos que agora xa só temos seis vértices aos que conectar con algún segmento

De continuarmos así, é evidente que o número total de segmentos que podemos trazar entre eses 8 puntos é $1+2+3+4+5+6+7=28$ polo que o número de diagonais serían $28-8=20$

Ao decatármonos de que cada segmento une dous puntos, veremos que estamos tratando co problema de como escoller dous elementos de entre 8. A este tipo de recontos chámaselle combinacións. Todas as posibles combinacións de dous elementos escollidos dentro dun conxunto de 8 pódense enumerar sistematicamente 

$$\begin{matrix} &  &  &  &  &  &12 \\  &  &  &  &  &23  &13 \\  &  &  &  &34  &24  & 14\\  &  &  &45  &35  & 25 &15 \\  &  & 56 &46  & 36 &26  &16 \\  &67  & 57 &47  & 37 &27  &17 \\ 78 &68  & 58 &48  &38  &28  &18 \end{matrix}$$

Cantas parellas vemos? Contando de esquerda a dereita $1+2+3+4+5+6+7$, ademais esta disposición forma unha escaleira, como a que repesentamos antes. Tamén poderiamos argumentar que cada un dos elementos pode emparellarse cos outros sete, co cal teriamos $8\cdot7$ parellas pero aparecerían duplicadas, de aí que o resultado teremos que dividilo por dous. 

Vemos repetido, unha e outra vez o mesmo argumento e en distintos contextos. Velaquí a condensación de todo o que estivemos estudando

$$1+2+3+...+n=\frac{n\left ( n+1 \right )}{2}$$

Ademais, en todo este proceso aprendimos que é moito mellor deixar esta fórmula para o final. Así é como se aprenden, e como se deberían ensinar, as matemáticas. 

A luz inúndao todo. (Continuará)

Algoritmo do produto do século XVI

Esta pretende ser a última entrada adicada ao Sumario Compendioso de Juan Díez, que foi identificado polo matemático e historiador David E. Smith como de orixe galega. Pódense seguir aquí todas as publicacións sobre este tema neste blogue:

• Juan Díez, quizais o primeiro matemático galego
• Os problemas alxébricos do "Sumario Compendioso" de Juan Díez
• Cuestións diofantinas do "Sumario Compendioso" de Juan Díez

Unha das "Regras comúns" que se explican nese libro é a adicada ao algortimo da multiplicación. Estamos moi afeitos a realizar os produtos tal e como aprendimos na escola e o habitual é que non nos cuestionemos esa serie de regras. Juan Díez explica como facer o produto de dous números. Faino recorrendo a un exemplo, o de $875\cdot 978$. O método consiste en ir multiplicando, de esquerda a dereita, cada unha das cifras do primeiro número, $875$, por todas e cada unha das cifras do segundo número, $978$. Iremos colocando os resultados de cada un destes produtos en columnas, correndo un lugar á dereita de cada vez. Isto é lóxico debido á notación posicional que usamos. Finalmente realizaremos a suma de todos os resultados. O mellor é ver en acción como se realiza este produto.

Hai que ter coidado cun aspecto que non está tratado neste exemplo. Pode darse o caso que un dos produtos parciais sexa de só unha cifra. Neste suposto debemos colocar o resultado como se tivese dúas. Por exemplo se un produto fose $2\cdot3=6$, para colocar ese $6$ obraríamos como se fose $06$.

Despois de visto este algoritmo, parecería máis lóxico que fose este o que se ensinara nas aulas de primaria pois permite unha xustificación máis clara do algoritmo.

Cuestións diofantinas do "Sumario Compendioso" de Juan Díez

Tal e como prometera na primeira entrada adicada ao Sumario Compendioso de Juan Díez, vou continuar debullando algúns aspectos dese libro. Neste caso abórdanse as páxinas tituladas Cadrados, que tratan sobre problemas diofantinos.

Primeira cuestión. Dáme un número que xuntándolle 15 faga un cadrado e restándolle 4 tamén sexa cadrado.

Regra. Suma 15 e 4, son 19. Engádelle 1, son 20. Toma a metade, que é 10. O seu cadrado, 10 veces 10 son 100. Disto resta 15 que son 85, e este é o número demandado do cal resta 4, que dá 81, cuxa raíz é 9.

No Liber quadratorum de Leonardo de Pisa, a segunda proposición di que calquera cadrado excede ao inmediatamente anterior na suma das súas raíces. En efecto, $n^{}-\left ( n-1 \right )^{2}=2n-1=\left ( n-1 \right )+n$.

Se aplicamos este resultado á primeira cuestión, temos que buscar un número intermedio entre dous cadrados consecutivos que diste 15 e 4 dos mesmos. A suma das distancias será a diferenza dos cadrados: $15+4=9=2n-1$. Se, como di Juan Díez, lle engadimos 1, obtemos $2n$.

Segunda cuestión. Dáme un número que xuntándolle 8 sexa cadrado e restándolle 8 fique cadrado. En maior cantidade dáme un número que xuntándolle 20 sexa un cadrado e restándolle 20 fique cadrado.

Regra. Toma a metade de 8, que é 4. Eleva ao cadrado, é 16, xúntalle 1, é 17 e este é o número demandado.[...] Toma a metade de 20, que é 10. Eleva ao cadrado, é 100, xúntalle 1 e fai 101 e este é o número demandado.

Os cadrados son $17-8=9=3^{2}$ e $17+8=25=5^{2}$ no primeiro caso e $101-20=81=9^{2}$ e $101+20=11^{2}$ no segundo. Nos dous os cadrados son da forma $\left ( n-1 \right )^{2}$ e $\left ( n+1 \right )^{2}$, de aí que a solución veña dada pola media $$x=\frac{\left ( n-1 \right )^{2}+\left ( n+1 \right )^{2}}{2}=n^{2}+1$$ Se lle chamamos $d$ á distancia entre o número buscado e calquera dos cadrados $\left ( n-1 \right )^{2}+2d=\left ( n+1 \right )^{2}$, de aí que $n=n=\frac{d}{2}$ e, polo tanto $x=\left ( \frac{d}{2} \right )^{2}+1$, que é a regra que dá Juan Díez.

Terceira cuestión. Unha persoa ten dúas cordas moi boas, danlle por elas 8 pesos, non as quere dar. Vén outro a compralas por varas de forma que por cada vara lle dá tantos tomíns como varas teña a corda. Despois de botar contas observa que este non lle dá máis que o primeiro. Demando cantas varas tiña cada corda.

David Eugene Smith explica a solución que se dá no Sumario compendioso da seguinte maneira. Sexan $x$, $y$, as lonxitudes (que neste problema son iguais aos prezos) de cada unha das cordas. Tendo en conta que 8 tomíns equivalen a un peso, o que se paga por elas son 64 tomíns. Se damos todos os valores en tomíns, o prezo das dúas cordas será $x^{2}+y^{2}=64=8^{2}$. Entón Díez emprega un método que non aceptariamos hoxe. Partindo de que $3^{2}+4^{2}=5^{2}$. aplica unha regra de 3 (!) entre estas expresións obtendo $\frac{x}{3}=\frac{8}{5}$, de aí que $x=4\frac{4}{5}$ e despois $y=64\frac{2}{5}$

Cuarta cuestión. Se che fose pedida esta cuestión: dáme un cadrado tal que restándolle unha certa candidade fique un cadrado e engadíndolla sexa tamén cadrado.

Lembremos que este é esencialmente o problema que Xoán de Palermo lle propuxo a Leonardo de Pisa e que sería o que daría lugar a que este escribira o Liber quadratorum. Do que se trata é de achar tres cadrados en progresión xeométrica. Na ligazón vese como o resolveu Fibonacci, a partir da definición dos congruum e os números congruentes con eles. Juan Díez dá un listrado destes valores e resolve o problema a partir deles. Aquí volvemos a ver a un Juan Díez coñecedor da terminoloxía e dos estudos dos cadrados feitos por Leonardo de Pisa.

Se aos congruos lle sumamos e restamos os congruentes, obtemos a terna de cadrados en progresión aritmética. No primeiro caso $25-24=1$, $25-24=49$. Resulta que $(1=1^{2},25=5^{2},49=7^{2})$ é unha das ternas buscadas. No segundo caso $100-96=4$ e $100+96=196$. Outra terna de cadrados en progresión xeométrica será $(4=2^{2},100=10^{2},196=14^{2})$

Curiosamente, así como podemos dar moitos exemplos de tres cadrados en progresión aritmética non é posible achar catro cadrados en progresión aritmética. Parece ser que Fermat estableceu este resultado nunha carta a Frenicle en 1640 pero que, como era o seu costume, non ofreceu ningunha demostración. Euler había de daría un resultado que levaría directamente á demostración, pero ata ben entrado o século XX non se ten coñecemento de que ninguén se volvera a preocupar deste teorema co fin de ofrecer unha demostración explícita. 

Quinta cuestión. Achar tres cadrados ou máis tales que sumados fagan un cadrado.

Nesta outra entrada explicamos como Fibonacci podía dar unha suma de $n$ cadrados que fose tamén un cadrado. Para is0 non tiña máis que aplicar recursivamente esta identidade para calqura número impar $x$: $$x^{2}=\left (\frac{x^{2}+1}{2}  \right )^{2}-\left (\frac{x^{2}-1}{2}  \right )^{2}$$

A resposta de Juan Díez é a mesma que a que acabamos de indicar, polo que volvemos a ver que coñecía os tópicos matemáticos desa altura.

Tomo o primeiro número cadrado impar, que é 9, ao cal resta un, quedan 8, toma a metade e cádrao, son 16 e isto é o segundo, axunta 9 e 16, son 25, [e agora repite o proceso], quita un, quedan 24, toma a metade, é 12, cádrao, son 144 e este é o terceiro. Se o queres ver suma 9 e 16 e 144, son 169, raíz dos cales é 13: e nota que por esta vía poderalo facer in infinitum.

O seguinte problema está relacionado con este.

Sexta cuestión. Digo que me deas un cadrado que quitándolle ou xuntándolle tres veces a súa raíz fagan un número cadrado.

Para resolvelo Díez aproveita a súa lista de números congruos. De feito el usa o primeiro da lista, aquel que nos dá $25-24=1$ e $25+24=49$. Teñamos presente que $24=3\cdot 8$, de aí que $5^{2}-3\cdot 8=1^{2}$. O problema estaría resolto se nesta igualdade, no canto dun $5^{2}$ tivese un $8^{2}$. Para aproveitar este feito multiplico a igualdade por $\frac{5^{2}}{8^{2}}$:

$$\frac{5^{2}}{8^{2}}\cdot 5^{2}-3\cdot 8\cdot \frac{5^{2}}{8^{2}}=\frac{5^{2}}{8^{2}}$$

$$\left (\frac{25}{8}  \right )^{2}-3\cdot \frac{25}{8}=\left ( \frac{5}{8} \right )^{2}$$

De aí que $\frac{25}{8}$ sexa a solución do problema proposto que se dá no Sumario Compendioso.

Os dous últimos problemas teñen unha redacción moi parecida. Por iso xa os damos xuntos.

Sétima cuestión. Anota isto, o cadrado de 2 é 4, o cadrado de 3 é 9, e a súa suma fai 13. Dáme outros dous números que non sexan nin 2 nin 3, tal que a suma dos seus cadrados sexa 13.

Oitava cuestión. O cadrado de 3 é 9, o cadrado de 4 é 16, e sumados, 25. Dáme outros números que non sexan nin 3 nin 4, tal que a suma dos seus cadrados sexa 25.

Está claro que as solucións terán que ser racionais.... e como a lonxitude a entrada xa vai sendo suficente, deixamos o comentario neste punto.