Nunca estudei a xeometría inversiva. O máis cerca que estiven diso foi nas clases de Álxebra II, no segundo cuso da carreira, cando traballamos a razón dobre. Aquel achegamento , facendo honra á denominación da materia, foi puramente alxébrico. Nesas clases nunca debuxamos unha circunferencia. Así, cando vexo algúns apuntes sobre ese tema ando sempre ás atoutiñadas, todo me sorprende.
Nunha entrada anterior xa se explicaba en que consistía a inversión dun plano mediante unha circunferencia. Recórdoo de seguido. Trátase dunha transformación do plano (agás un punto) en si mesmo. Dada unha circunferencia, (que chamaremos circunferencia inversiva) de centro O (centro de inversión) e raio R construiremos a inversión así:
Se $P$ é un punto do círculo de centro $O$ e raio $R=OT$ trazamos a semirecta $OP$ e a súa perpendicular polo punto $P$. Esta perpendicular cortará en dous puntos á circunferencia. A tanxente nun destes puntos cortará a semirecta $OP$ nun punto $P'$ que será a inversión de $P$
No caso de que $P$ fique fóra do círculo a obtención de $P'$ sería semellante. Desde $P$ trazamos unha das tanxentes á circunferencia $PT$. Despois trázase a perpendicular a $OP$ por $T$ e obtemos $P'$
En calquera caso o inverso dun punto $P$ respecto dunha circunferencia de centro $O$ e raio $R$ é outro punto $P'$ na semirecta $OP$ tal que $OP\cdot OP'=R^{2}$ Son bastante evidentes as seguintes propiedades:
- O inverso do inverso é o propio punto
- O inverso dun punto interior á circunferencia fica fóra da mesma e viceversa.
- Os únicos puntos auto-inversos son os da circunferencia
Na entrada á que facía referencia anteriormente deducíranse algunhas propiedades da inversión usando un método un tanto estrafalario (mediante o uso da proxección estereográfica). Alí establecimos os seguintes resultados:
- A inversión conserva os ángulos
- A inversa dunha recta que pasa por O é a propia recta (sempre que omitamos o propio punto O, que é o único que non ten imaxe)
- A inversión transforma circunferencias que non pasan por O en circunferencias
- A inversión transforma circunferencias que pasan por O en rectas.
Consideremos unha recta $a$ que non pase por $O$. Tracemos desde $O$ a perpendicular a $a$, $=OA$. Sexa $A'$ a inversa de $A$. Debuxemos a circunferencia $\alpha $ de diámetro $OA$. Desde un punto $P\in a$ trazamos o segmento $OP$ que cortará a $\alpha $ nun punto $P'$.
Os triángulos $\triangle OP'A'$ e $\triangle OPA$ son semellantes xa que comparte o ángulo en O e ambos teñen ademais un ángulo recto. De aí que tamén $$\frac{OP}{OA}=\frac{OA'}{OP'}\Rightarrow OP\cdot OP'=OA\cdot OA'=R^{2}$$
Entón $P'$ é o inverso de P. Recíprocamente calquera punto da circunferencia $\alpha$ invértese noutro da recta $a$
A lonxitude dun segmento invertido
Seguindo o libro de Coxeter e Greitzer abordaremos agora un teorema que explica como se modifica a distancia mediante a inversión.
Fórmula da lonxitude dun segmento invertido. Se unha circunferencia $\omega$ de centro $O$ e raio $R$ inverte os puntos $A$ e $B$ en $A'$ e $B'$, as distancias verifican a seguinte relación $$A'B'=\frac{R^{2}\cdot AB}{OA\cdot OB}$$
Sexa $A'$ inverso de $A$: $OA\cdot OA'=R^{2}$
Sexa $B'$ inverso de $B$: $OB\cdot OB'=R^{2}$
Entón $OA\cdot OA'=OB\cdot OB'$ polo que e $$\frac{OA}{OB}=\frac{OB'}{OA'}$$
Daquela os triángulos $\triangle OAB$ e $\triangle OA'B'$ son semellantes pois o ángulo en O é común e os lados que o determinan son proporcionais (aplicamos o chamado criterio LAL). Polo tanto temos tamén que $$\frac{A'B'}{AB}=\frac{OA'}{OB}=\frac{OA\cdot OA'}{OA\cdot OB}=\frac{R^{2}}{OA\cdot OB}$$
Despexando, obtemos a igualdade prometida: $$A'B'=\frac{R^{2}\cdot AB}{OA\cdot OB}$$
Un regalo: o teorema de Ptolomeo
Hai moitas demostracións do teorema de Ptolomeo. Algunhas teñen base trigonométrica, outras usan a semellanza de triángulos. No libro que vimos mencionando demóstrase este teorema usando a recta de Simson-Wallace (para este tema ver estas outras entradas neste mesmo blogue [1] e [2]). Resulta que tamén hai unha demostración inversiva, ademais é directa e simple.
Antes de nada lembremos que un cuadrilátero cíclico é aquel que ten os catro vértices nunha mesma circunferencia. Sabendo isto podemos enunciar o
Teorema de Ptolomeo. Se ABCD é un cuadrilátero cíclico, a suma dos produtos dos pares de lados opostos é igual ao produto das diagonais, isto é: $AC\cdot BD=AD\cdot BC+AB\cdot BC$
Sexa $\alpha$ a circunferencia pola que pasan os catro vértices do cuadrilátero. Tomando o vértice $A$ como centro, construímos outra circunferencia $\omega$ que conteña ao cuadrilátero. Agora, como os outros vértices, $B$, $C$ e $D$ están en $\alpha$, unha circunferencia que pasa polo centro de inversión, se os invertemos, as súas imaxes $B'$, $C'$ e $D'$ ficarán todas nunha recta. Velaí que $$B'D'=B'C'+C'D'$$
Fagamos agora uso da fórmula, dada anteriormente, que nos dá a distancia dun segmento invertido:$$\frac{R^{2}\cdot BD}{AB\cdot AD}=\frac{R^{2}\cdot BC}{AB\cdot AC}+\frac{R^{2}\cdot CD}{AC\cdot AD}$$
Eliminando $R^{2}$ e sacando denominadores facendo uso de que o seu mínimo común múltiplo é $AB\cdot AC\cdot AD$:
$$AB\cdot BD=AD\cdot BC+AB\cdot CD$$
O recíproco do teorema de Ptolomeo tamén se verifica, isto é:
Recíproco do teorema de Ptolomeo. Se ABCD é un cuadrilátero tal que: $AC\cdot BD=AD\cdot BC+AB\cdot BC$, entón ABCD é un cuadrilátero cíclico.Por outra banda, dados catro puntos calquera, sempre se verificaría a desigualdade, coñecida tamén como desigualdade de Ptolomeo: $$AB\cdot BD\leq AD\cdot BC+AB\cdot CD$$
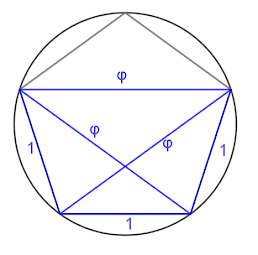
Como colofón citaremos a seguinte aplicación do teorema de Ptolomeo. Consideremos o pentágono regular de lado unidade. As súas diagonais son evidentemente iguais (son a base de triángulos isósceles de lado 1); poñamos que miden $\varphi$ Desbotando por exemplo o vértice superior quédanos un cuadrilátero cícliclo.
Se lle aplicamos a este cuadrilátero o teorema de Ptolomeo teremos que $$\varphi \cdot \varphi =1\cdot \varphi +1$$
$$\varphi ^{2}=\varphi +1$$
Esta é unha ecuación doada de resolver, ou de recoñecer.


Ningún comentario:
Publicar un comentario