NOTA previa: moléstame moito escribir *círculo cando me estou referindo a unha circunferencia. Con todo, vouno facer porque ese parece ser o terríbel costume instaurado na literatura que trata dos elementos xeográficos e astronómicos.
Coordenadas xeográficas
Consideraremos a Terra como unha esfera que xira arredor do eixo imaxinario que pasa polos polos (Polo Norte:P e Polo Sur: P') [nota aparte:encántame escribir unha palabra varias veces seguidas nunha frase con sentido]. O cículo máximo perpendicular a este eixo é o
ecuador EE'
. Os círculos paralelos ao ecuador chámanse precisamente
paralelos. Cada un dos paralelos estará a unha distancia angular CTE denominada
latitude, un ángulo φ que se mide entre 0º e 90º no hemisferio norte e no mesmo rango, pero con valores negativos, no hemisferio sur. Hai dous paralelos destacados, que ata reciben nome propio. O de latitude +23º26' é o chamado
trópico de Cáncer, e o de latitude -23º26' denomínase
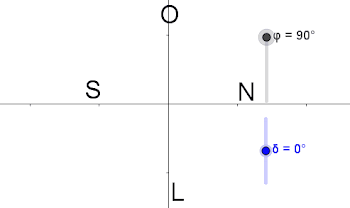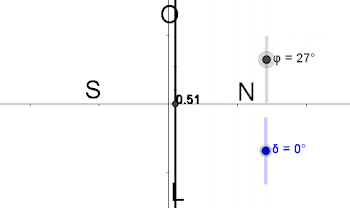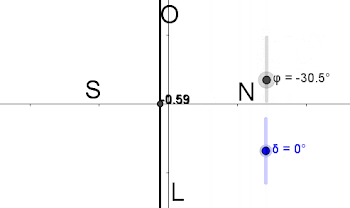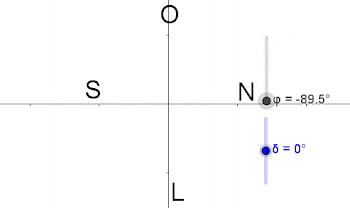
trópico de Capricornio.Máis abaixo falaremos das coordenadas celestes. Nese momento seguiremos a falar do eixo do mundo PP'. Agora P indicaranos o polo norte na esfera celeste. Resulta que nun punto da Terra no paralelo de latitude φ, a altura (ángulo entre o ecuador e o punto) do polo norte será precisamente φ: hP=φ
Para determinar un punto na esfera cómpre outra coordenada. Se a latitude se determina a partir do círculo máximo do ecuador, a lonxitude determinarase tomando como referencia un dos meridianos ou círculos máximos que pasan polos polos [outra vez]. Tómase como referencia o meridiano que pasa polo Observatorio Real Observatorio de Greenwich (en Londres, Inglaterra). A distancia angular respecto deste meridiano é a lonxitude λ. Toma valores positivos cara o leste do meridiano, ata os 180º, e negativos cara o oeste. Se na figura 1 consideramos o meridiano PGP' como o de Greenwich, a lonxitude do punto T sería o ángulo λ entre este meridiano e o meridiano PTP'.
Por poñer un exemplo, o IES Antón Losada Diéguez (A Estrada) ten como coordenadas xeográficas unha latitude φ=42º 41' 33,5''= 42,69264 e uñha lonxitude λ=-8º 30' 24''=-8,50667
Pasemos agora ao estudo das coordenadas na esfera celeste.
Sistema de coordenadas horizontais
Para determinar un punto na esfera celeste teremos como referencia o
plano do horizonte, o plano NLSO. A recta perpendicular a este plano e na que se encontra o observador denomínase
liña vertical. Esta liña cortará en dous puntos á esfera celeste. O punto Z situado enriba do observador C chámase
cénit e Z', situado debaixo, recibe o nome de
nadir. Os círculos máximos que teñen diámetro ZCZ' denomínanse
círculos verticais.
Unha das coordenadas horizontais dun astro X será a altura h: o arco AX do círculo vertical AXZ. Toma valores entre 0º e 90º na parte visible da esfera celeste. Os valores negativos ata -90º correspóndense ás alturas na dirección do nadir. Alternativamente pódese dar a distancia cenital z: o arco ZX (que se mide entre 0º e 180º). Fica claro que se verifica que z+h=90º
Un círculo paralelo ao plano do horizonte denomínase almicantarat. Todos os puntos dun almicantarat teñen a mesma altura.
A outra coordenada horizontal é o acimut a: o ángulo SCA entre o círculo vertical do observador e o do astro X, medido desde o sur en dirección oeste. Pode tomar valores entre 0º e 360º. Algunhas veces podemos ver definido o acimut partindo do norte, especialmente en xeodesia. Os puntos dun mesmo círculo vertical compartirán o mesmo acimut (土180º).
Polo movemento diario da Terra, unha estrela estará cambiando continuamente de coordenadas horizontais. Isto é unha desventaxa.
Primeiro sistema de coordenadas ecuatoriais
Tal e como anunciamos, denominaremos eixo do mundo PP' ao que une os polos. O círculo máximo perpendicular a PP' será o
ecuador celeste QQ'. A
declinación (ou latitude celeste) δ dun punto X situado sobre a esfera celeste é o ángulo que forma o raio vector CX co plano ecuatorial QQ'. Toma valores entre 0º e 90º para as estrelas do hemisferio boreal e terá valores negativos para as do hemisferio austral. A veces subsitúese esta coordenada polo arco p=PX, denominado
distancia polar. Verifícase que p+δ=90º.
Os círculos máximos de diámetro PP' chámanse círculos horarios. A segunda coordenada obterase ao escoller o círculo horario QPQ'P'. Se medimos desde Q, sobre o ecuador celeste, o ángulo ata o círculo horario do punto X, teremos a coordenada t denominada ángulo horario. Este ángulo mídese desde Q cara o occidente para valores positivos de ata 180º. A dirección contraria resérvase para os valores negativos.
Segundo sistema de coordenadas ecuatoriais
A
eclíptica é o plano ε'γεΩ no que se move o Sol. Forma un ángulo de 23º 26' co ecuador celeste e intersécao en dous puntos: o punto vernal ou punto Aries γ que determina o equinocio de primavera e o punto Libra Ω, que é aquel polo que pasa o Sol no equinocio de outono.
Agora podemos falar dun un segundo sistema de coordenadas ecuatoriais. Tal e como indica o seu nome, tómase como referencia o ecuador celeste. De aí que unha das coordenadas sexa a antes mencionada declinación δ. O outro plano de referencia será a eclíptica, de aí que a outra coordenada deste sistema sexa a ascensión recta α que será o arco sobre o ecuador celeste desde o punto Aries ata o círculo horario do astro. Toma valores ata os 360º.
O triángulo paraláctico.
Xa sabemos que as coordenadas horizontais están cambiando contiuamente co movemento diurno da Terra.. Pola contra as ecuatoriais permanecen fixas. Tamén é certo que as primeiras son máis intuitivas, de feito historicamente preceden ás segundas. Imos intentar establecer un sistema de cambio entre unhas es outras. Estas trasformacións poden facerse mediante o chamado
triángulo paraláctico. Trátase dun triángulo esférico ZPX que ten como vértices o cénit do punto de observación Z, o polo norte celeste P e a estrela ou punto da esfera celeste X.
O lado PZ é o ángulo complementario da latitude do punto de observación: PZ=90-φ
O lado PX é o ángulo completentario da declinación do punto X: PX=90-δ
O lado ZX é o ángulo complementario da altura do punto X: ZX=90-h=z
O ángulo PZX é o ángulo suplementario do acimut de X: PZX=180-a
O ángulo ZPX é o ángulo horario t.
Tomando a distancia cenital z=90-h e aplicando as fórmulas do coseno e dos senos da trigonometría esférica ao triángulo paraláctico teremos:
$$cos\left ( 90-\delta \right )=cos\left ( 90-\varphi \right )senzsen\left ( 180-a \right )$$ $$sen\left ( 90-\delta \right )sent=senzsen\left ( 180-a \right )$$ $$sen\left ( 90-\varphi \right )cost=sen\left ( 90-\varphi \right )cosz-cos\left ( 90-\varphi \right )senzcos\left ( 180-a \right )$$
Polas propiedades básicas das razóns trigonométricas quedarían reducidas ao seguinte grupo de fórmulas que, a partir das coordenadas horizontais (z,a) nos darían as ecuatoriais (δ, t):
$$sen\delta =sen\varphi \ cosz-cos\varphi \ senz\ cosa$$ $$cos\delta \ sent=senz\ sena$$ $$cos\delta \ cost=cos\varphi \ cosz + sen\varphi\ senz\ cosa$$
Aplicando outra vez as fórmulas dos senos e coseno da trigonometría esférica ao triángulo paraláctico:
$$cosz=cos\left ( 90-\varphi \right )\ cos\left ( 90-\delta \right ) + sen\left ( 90-\varphi \right )\ sen\left ( 90-\delta \right )\ cost$$ $$senz\ sen\left ( 180-a \right )=sen\left ( 90-\delta \right )\ sent$$ $$senz\ cos\left ( 180-a \right )=sen\left ( 90-\varphi \right )\cos\left ( 90-\delta \right )-cos\left ( 90-\varphi \right )\ sen\left ( 90-\delta \right )\ cost$$
Simplificando obtemos as fórmulas que nos dan o cambio das coordenadas ecuatoriais (δ, t) ás horizontais (z,a):
$$cosz=sen \varphi \ sen\delta +cos\varphi \ cos\delta \ cost$$ $$senz\ sena=cos\delta \ sent$$ $$senz\ cosa=-cos\varphi \ sen\delta +sen\varphi \ cos\delta \ cost$$